
ЁОЬтФПЁПЮЊЛКНтгЭМлЩЯеЧИјГізтГЕД§вЕДјРДЕФГЩБОбЙСІЃЌФГзд2018Фъ11дТ17ШеЦ№ЃЌЕїећГізтГЕдЫМлЃЌЕїећЗНАИМћЯТСаБэИёМАЭМЯѓЃЈЦфжаaЃЌbЃЌcЮЊГЃЪ§ЃЉ
ааЪЛТЗГЬ | ЪеЗбБъзМ | |
ЕїМлЧА | ЕїМлКѓ | |
ВЛГЌЙ§3kmЕФВПЗж | Ц№ВНМл6дЊ | Ц№ВНМлa дЊ |
ГЌЙ§3kmВЛГЌГі6kmЕФВПЗж | УПЙЋРя2.1дЊ | УПЙЋРяbдЊ |
ГЌГі6kmЕФВПЗж | УПЙЋРяcдЊ | |
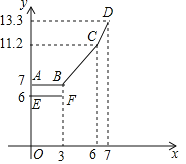
ЩшааЪЛТЗГЬxkmЪБЃЌЕїМлЧАЕФдЫМлy1ЃЈдЊЃЉЃЌЕїМлКѓЕФдЫМлЮЊy2ЃЈдЊЃЉШчЭМЃЌелЯпABCDБэЪОy2гыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌЯпЖЮEFБэЪОЕБ0ЁмxЁм3ЪБЃЌy1гыxЕФКЏЪ§ЙиЯЕЪНЃЌИљОнЭМБэаХЯЂЃЌЭъГЩЯТСаИїЬтЃК
ЃЈ1ЃЉЬюПеЃКa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЌc=ЁЁ ЁЁЃЎ
ЃЈ2ЃЉаДГіЕБxЃО3ЪБЃЌy1гыxЕФЙиЯЕЃЌВЂдкЩЯЭМжаЛГіИУКЏЪ§ЕФЭМЯѓЃЎ
ЃЈ3ЃЉКЏЪ§y1гыy2ЕФЭМЯѓЪЧЗёДцдкНЛЕуЃПШєДцдкЃЌЧѓГіНЛЕуЕФзјБъЃЌВЂЫЕУїИУЕуЕФЪЕМЪвтвхЃЌШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ7ЃЌ1.4ЃЌ2.1ЃЛЃЈ2ЃЉy1=2.1xЉ0.3ЃЛЭМЯѓМћНтЮіЃЛЃЈ3ЃЉКЏЪ§y1гыy2ЕФЭМЯѓДцдкНЛЕуЃЈ![]() ЃЌ9ЃЉЃЛЦфвтвхЮЊЕБ x<
ЃЌ9ЃЉЃЛЦфвтвхЮЊЕБ x<![]() ЪБЪЧЗНАИЕїМлЧАКЯЫуЃЌЕБx>
ЪБЪЧЗНАИЕїМлЧАКЯЫуЃЌЕБx>![]() ЪБЗНАИЕїМлКѓКЯЫуЃЎ
ЪБЗНАИЕїМлКѓКЯЫуЃЎ
ЁОНтЮіЁПЃЈ1ЃЉaгЩЭМПЩжБНгЕУГіЃЛbЁЂcИљОнЃКдЫМлЁТТЗГЬ=ЕЅМлЃЌДњШыЪ§жЕЃЌЧѓГіМДПЩЃЛ
ЃЈ2ЃЉЕБxЃО3ЪБЃЌy1гыxЕФЙиЯЕЃЌгЩСНВПЗжзщГЩЃЌЕквЛВПЗжЮЊЦ№ВНМл6ЃЌЕкЖўВПЗжЮЊЃЈxЉ3ЃЉЁС2.1ЃЌЫљвдЃЌСНВПЗжЯрМгЃЌОЭПЩЕУЕНКЏЪ§ЪНЃЌВЂПЩЛГіЭМЯѓЃЛ
ЃЈ3ЃЉЕБy1=y2ЪБЃЌНЛЕуДцдкЃЌЧѓГіxЕФжЕЃЌдйДњШыЦфжавЛИіЪНзгжаЃЌОЭФмЕУЕНyжЕЃЛyжЕЕФвтвхОЭЪЧжИдЫМл.
ЂйгЩЭМПЩжЊЃЌa=7дЊЃЌ
b=ЃЈ11.2Љ7ЃЉЁТЃЈ6Љ3ЃЉ=1.4дЊЃЌ
c=ЃЈ13.3Љ11.2ЃЉЁТЃЈ7Љ6ЃЉ=2.1дЊЃЌ
ЙЪД№АИЮЊ7ЃЌ1.4ЃЌ2.1ЃЛ
ЂкгЩЭМЕУЃЌЕБxЃО3ЪБЃЌy1гыxЕФЙиЯЕЪНЪЧЃК
y1=6+ЃЈxЉ3ЃЉЁС2.1ЃЌ
ећРэЕУЃЌy1=2.1xЉ0.3ЃЌ
КЏЪ§ЭМЯѓШчЭМЫљЪОЃК
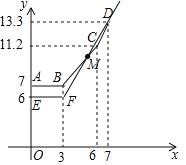
ЂлгЩЭМЕУЃЌЕБ3ЃМxЃМ6ЪБЃЌy2гыxЕФЙиЯЕЪНЪЧЃК
y2=7+ЃЈxЉ3ЃЉЁС1.4ЃЌ
ећРэЕУЃЌy2=1.4x+2.8ЃЛ
ЫљвдЃЌЕБy1=y2ЪБЃЌНЛЕуДцдкЃЌ
МДЃЌ2.1xЉ0.3=1.4x+2.8ЃЌ
НтЕУЃЌx=![]() ЃЌy=9ЃЛ
ЃЌy=9ЃЛ
ЫљвдЃЌКЏЪ§y1гыy2ЕФЭМЯѓДцдкНЛЕуЃЈ![]() ЃЌ9ЃЉЃЛ
ЃЌ9ЃЉЃЛ
ЦфвтвхЮЊЕБ x<![]() ЪБЪЧЗНАИЕїМлЧАКЯЫуЃЌЕБ x>
ЪБЪЧЗНАИЕїМлЧАКЯЫуЃЌЕБ x>![]() ЪБЗНАИЕїМлКѓКЯЫуЃЎ
ЪБЗНАИЕїМлКѓКЯЫуЃЎ


 АйЗжбЇЩњзївЕБОЬтСЗЭѕЯЕСаД№АИ
АйЗжбЇЩњзївЕБОЬтСЗЭѕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФЖЏЕуЃЈВЛКЭ
ЩЯЕФЖЏЕуЃЈВЛКЭ![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌ
жиКЯЃЉЃЌ![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() .
.

ЃЈ1ЃЉЕБЕу![]() дкБп
дкБп![]() ЩЯЪБЃЌЧѓжЄЃК
ЩЯЪБЃЌЧѓжЄЃК![]()
ЃЈ2ЃЉШєЕу![]() дк
дк![]() ЕФбгГЄЯпЩЯЪБЃЌЃЈ1ЃЉЕФНсТлЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыЛГіЭМаЮЃЈВЛаДЛЗЈЃЌЛГіЪОвтЭМЃЉЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіе§ШЗНсТл.
ЕФбгГЄЯпЩЯЪБЃЌЃЈ1ЃЉЕФНсТлЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧыЛГіЭМаЮЃЈВЛаДЛЗЈЃЌЛГіЪОвтЭМЃЉЃЛШєВЛГЩСЂЃЌЧыжБНгаДГіе§ШЗНсТл.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() жаЃЌ
жаЃЌ![]() ЖШЃЌ
ЖШЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЁЃЧѓжЄЃК
ЁЃЧѓжЄЃК
ЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ![]() ЮЊЕШбќжБНЧШ§НЧаЮЁЃ
ЮЊЕШбќжБНЧШ§НЧаЮЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЁїABCФкНггкЁбOЃЌOC=6cmЃЌAC=![]() cmЃЌдђЁЯBЕШгкЁЁ ЁЁЃЎ
cmЃЌдђЁЯBЕШгкЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкАыОЖЮЊ4ЕФЁбOжаЃЌдВаФНЧЁЯAOB=90ЁуЃЌвдАыОЖOAЁЂOBЕФжаЕуCЁЂFЮЊЖЅЕузїОиаЮCDEFЃЌЖЅЕуDЁЂEдкЁбOЕФСгЛЁ![]() ЩЯЃЌOMЁЭDEгкЕуMЃЎЪдЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎЃЈНсЙћБЃСєІаЃЉ
ЩЯЃЌOMЁЭDEгкЕуMЃЎЪдЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎЃЈНсЙћБЃСєІаЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁЖОХеТЫуЪѕЁЗЬсЙЉСЫаэЖрећЙДЙЩЪ§ЃЌШч![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕШЕШЃЌВЂАбвЛзщЙДЙЩЪ§жазюДѓЕФЪ§ГЦЮЊЁАЯвЪ§ЁБ.КѓШЫдкДЫЛљДЁЩЯНјвЛВНбаОПЃЌЕУЕНШчЯТЙцТЩЃКШє
ЕШЕШЃЌВЂАбвЛзщЙДЙЩЪ§жазюДѓЕФЪ§ГЦЮЊЁАЯвЪ§ЁБ.КѓШЫдкДЫЛљДЁЩЯНјвЛВНбаОПЃЌЕУЕНШчЯТЙцТЩЃКШє![]() ЪЧДѓгк1ЕФЦцЪ§ЃЌАбЫќЦНЗНКѓВ№ГЩЯрСкЕФСНИіећЪ§ЃЌФЧУД
ЪЧДѓгк1ЕФЦцЪ§ЃЌАбЫќЦНЗНКѓВ№ГЩЯрСкЕФСНИіећЪ§ЃЌФЧУД![]() гыетСНИіећЪ§ЙЙГЩвЛзщЙДЙЩЪ§ЃЛШє
гыетСНИіећЪ§ЙЙГЩвЛзщЙДЙЩЪ§ЃЛШє![]() ЪЧДѓгк2ЕФХМЪ§ЃЌАбЫќГ§вд2КѓдйЦНЗНЃЌШЛКѓАбетИіЦНЗНЪ§ЗжБ№Мѕ1ЃЌМгlЕУЕНСНИіећЪ§ЃЌФЧУД
ЪЧДѓгк2ЕФХМЪ§ЃЌАбЫќГ§вд2КѓдйЦНЗНЃЌШЛКѓАбетИіЦНЗНЪ§ЗжБ№Мѕ1ЃЌМгlЕУЕНСНИіећЪ§ЃЌФЧУД![]() гыетСНИіећЪ§ЙЙГЩвЛзщЙДЙЩЪ§.гЩЩЯЪіЗНЗЈЕУЕНЕФЙДЙЩЪ§ГЦЮЊЁАгЩ
гыетСНИіећЪ§ЙЙГЩвЛзщЙДЙЩЪ§.гЩЩЯЪіЗНЗЈЕУЕНЕФЙДЙЩЪ§ГЦЮЊЁАгЩ![]() ЩњГЩЕФЙДЙЩЪ§ЁБ.ШєЁАгЩ9ЩњГЩЕФЙДЙЩЪ§ЁБЕФЁАЯвЪ§ЁАМЧЮЊ
ЩњГЩЕФЙДЙЩЪ§ЁБ.ШєЁАгЩ9ЩњГЩЕФЙДЙЩЪ§ЁБЕФЁАЯвЪ§ЁАМЧЮЊ![]() ЃЌЁАгЩ20ЩњГЩЕФЙДЙЩЪ§ЁБЕФЁАЯвЪ§ЁАМЧЮЊ
ЃЌЁАгЩ20ЩњГЩЕФЙДЙЩЪ§ЁБЕФЁАЯвЪ§ЁАМЧЮЊ![]() ЃЌдђ
ЃЌдђ![]() __________ЃЎ
__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
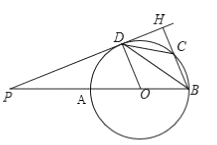
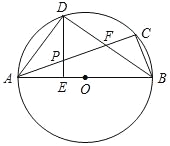
ЁОЬтФПЁПШчЭМЃЌдкЁбOжаЃЌЕуPЮЊжБОЖBAбгГЄЯпЩЯвЛЕуЃЌPDЧаЁбOгкЕуDЁЂЙ§ЕуBзїBHЁЭPHЃЌЕуHЮЊДЙзуЃЌBHНЛЁбOгкЕуCЃЌСЌНгBDЃЌCDЃЎ
ЃЈ1ЃЉЧѓжЄЃКBDЦНЗжЁЯABHЃЛ
ЃЈ2ЃЉШєCD=2ЃЌЁЯABD=30ЁуЃЌЧѓЁбOЕФжБОЖЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
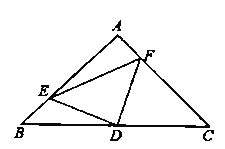
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABCФкНггкЁбOЃЌABЮЊжБОЖЃЌЁЯCBAЕФЦНЗжЯпНЛACгкЕуFЃЌНЛЁбOгкЕуDЃЌDEЁЭABгкЕуEЃЌЧвНЛACгкЕуPЃЌСЌНсADЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯDAC=ЁЯDBAЃЛ
ЃЈ2ЃЉЧѓжЄЃКPD=PFЃЛ
ЃЈ3ЃЉСЌНгCDЃЌШєCDЉ3ЃЌBDЉ4ЃЌЧѓЁбOЕФАыОЖКЭDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЕу![]() ЃЌЕу
ЃЌЕу![]() .
.
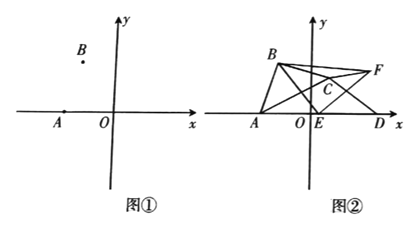
ЃЈ1ЃЉдкЭМЂйжаЕФ![]() жсЩЯЧѓзїЕу
жсЩЯЧѓзїЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЕФжЕзюаЁЃЛ
ЕФжЕзюаЁЃЛ
ЃЈ2ЃЉШє![]() ЪЧвд
ЪЧвд![]() ЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу
ЮЊбќЕФЕШбќжБНЧШ§НЧаЮЃЌЧыжБНгаДГіЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЃЈВЛгыЕу
ЃЈВЛгыЕу![]() жиКЯЃЉЪЧ
жиКЯЃЉЪЧ![]() жсЩЯвЛИіЖЏЕуЃЌЕу
жсЩЯвЛИіЖЏЕуЃЌЕу![]() ЪЧ
ЪЧ![]() жаЕуЃЌСЌНс
жаЕуЃЌСЌНс![]() ЃЌАб
ЃЌАб![]() ШЦзХЕу
ШЦзХЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЈМД
ЃЈМД![]() ЃЌ
ЃЌ![]() ЃЉЃЌСЌНс
ЃЉЃЌСЌНс![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЪдВТЯы
ЃЌЪдВТЯы![]() ЕФЖШЪ§ЃЌВЂИјГіжЄУї.
ЕФЖШЪ§ЃЌВЂИјГіжЄУї.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com