
【题目】已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧![]() 上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)
上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)

【答案】4π﹣![]() .
.
【解析】
阴影部分的面积等于扇形OAB的面积减去等腰直角三角形OAB的面积再减去矩形PDEQ的面积.求得相关的线段后即可得解.
∵∠AOB=90°,
∴扇形AOB的面积=![]() .
.
∵C、F分别为OA、OB的中点,OA=OB=4,
∴OC=OF=2,CF=![]() .
.
∴CF平行且等于![]() AB.
AB.
∴AB=2CF=![]() .
.
∴CF∥AB∥DE,
∴CD⊥AB,FE⊥AB.
∵OM⊥DE,
∴OM⊥AB.
∵△AON为等腰直角三角形,且OA=4,
∴ON=![]() .连接OD,
.连接OD,
∵DM=ME=![]() ,
,
∴OM=![]() .
.
∴MN=PD=QE=![]() ﹣
﹣![]() .
.
∴矩形PDEQ的面积=![]() ×(
×(![]() ﹣
﹣![]() )=
)=![]() -8
-8
∴S阴影=S扇形AOB﹣S△AOB﹣S矩形PDEQ=4π﹣![]()


科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点P为直径BA延长线上一点,PD切⊙O于点D、过点B作BH⊥PH,点H为垂足,BH交⊙O于点C,连接BD,CD.
(1)求证:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
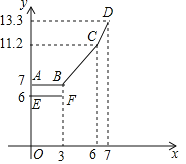
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一个动点.
(1)在图中标出圆心P位置,写出点P坐标;
(2)Q点在圆上坐标为何值时,△ABQ是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 交
交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,平行于
两点,平行于![]() 轴的直线
轴的直线![]() 从点
从点![]() 开始以每秒
开始以每秒![]() 个单位的速度向
个单位的速度向![]() 轴的负方向运动,直线
轴的负方向运动,直线![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设直线
,设直线![]() 的运动时间为
的运动时间为![]() 秒.
秒.

![]() 求线段
求线段![]() 的长.
的长.
![]() 若
若![]() 为直线
为直线![]() 上一动点,将
上一动点,将![]() 沿着
沿着![]() 翻折,当点
翻折,当点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上时,求直线
上时,求直线![]() 的解析式.
的解析式.
![]() 若
若![]() 为
为![]() 的中点,当
的中点,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于![]() 的分式方程
的分式方程![]() .
.
(1)当![]() ,
,![]() 时,求分式方程的解;
时,求分式方程的解;
(2)当![]() 时,求
时,求![]() 为何值时分式方程
为何值时分式方程![]() 无解:
无解:
(3)若![]() ,且
,且![]() 、
、![]() 为正整数,当分式方程
为正整数,当分式方程![]() 的解为整数时,求
的解为整数时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com