
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的动点(不和
上的动点(不和![]() 、
、![]() 重合),
重合),![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.

(1)当点![]() 在边
在边![]() 上时,求证:
上时,求证:![]()
(2)若点![]() 在
在![]() 的延长线上时,(1)的结论是否成立?若成立,请画出图形(不写画法,画出示意图);若不成立,请直接写出正确结论.
的延长线上时,(1)的结论是否成立?若成立,请画出图形(不写画法,画出示意图);若不成立,请直接写出正确结论.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
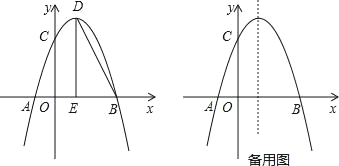
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接DB.
(1)求此抛物线的解析式及顶点D的坐标;
(2)点M是抛物线上的动点,设点M的横坐标为m.
①当∠MBA=∠BDE时,求点M的坐标;
②过点M作MN∥x轴,与抛物线交于点N,P为x轴上一点,连接PM,PN,将△PMN沿着MN翻折,得△QMN,若四边形MPNQ恰好为正方形,直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
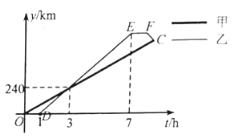
【题目】甲、乙两车从![]() 地出发,沿同一条笔直的公路匀速驶向
地出发,沿同一条笔直的公路匀速驶向![]() 地,乙车先到达
地,乙车先到达![]() 地并停留
地并停留![]() 后,再以原速按原路返回,直至与甲车相遇.已知两车到
后,再以原速按原路返回,直至与甲车相遇.已知两车到![]() 地的距离
地的距离![]()
![]() 与甲车出发的时间
与甲车出发的时间![]()
![]() 之间的函数关系分别如图中线段
之间的函数关系分别如图中线段![]() 和折线
和折线![]() 所示,则图中点
所示,则图中点![]() 的坐标为_______________.
的坐标为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论中,错误的有( )
①在Rt△ABC中,已知两边长分别为3和4,则第三边的长为5;
②△ABC的三边长分别为AB,BC,AC,若![]() +
+![]() =
=![]() ,则∠A=90°;
,则∠A=90°;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④若三角形的三边长之比为3:4:5,则该三角形是直角三角形.
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
![]() 如图①,在
如图①,在![]() 中,
中,![]() 为角平分线,
为角平分线,![]() ,
,![]() ,求证:
,求证:![]() 是
是![]() 的完美分割线;
的完美分割线;
![]() 如图②,在
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() 是以
是以![]() 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线![]() 的长.
的长.
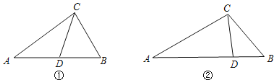
查看答案和解析>>
科目:初中数学 来源: 题型:
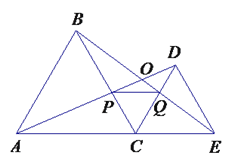
【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
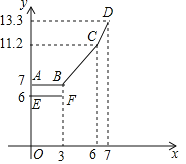
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com