
【题目】若△ABC内接于⊙O,OC=6cm,AC=![]() cm,则∠B等于 .
cm,则∠B等于 .
【答案】60°或120°;
【解析】
①连接OA,OC,过O作OD⊥AC于D,求出CD、AD,由勾股定理求出OD,求出∠ACO推出∠AOC=120°,根据圆周角定理求出∠B=![]() ∠AOC,代入求出即可.②同样可求出∠D=60°,根据圆内接四边形性质求出∠ABC=120°.
∠AOC,代入求出即可.②同样可求出∠D=60°,根据圆内接四边形性质求出∠ABC=120°.
如图1所示:
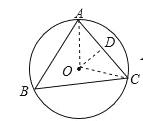
①连接OA,OC,过O作OD⊥AC于D,
∵OD⊥AC,OD过圆心O,
∴AD=CD=![]() AC=3
AC=3![]() ,
,
由勾股定理得:OD=![]() =3,
=3,
即OD=![]() OC,
OC,
∴∠DCO=30°,∠COD=60°,
同理∠AOD=60°,
∵∠B=![]() ∠AOC,
∠AOC,
∴∠B=60°.
②如图所示:
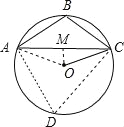
∵由垂径定理得CM═3![]() ,OC=6,由勾股定理得:OM=3,
,OC=6,由勾股定理得:OM=3,
∴∠OCM=30°,
∴∠MOC=60°,
∴∠AOC=2∠MOC=120°,
由圆周角定理得:∠D=60°,
∵A、D、C、B四点共圆,
∴∠ABC=120°,
故答案是:60°或120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:直线![]() ,点
,点![]() ,
,![]() 分别是直线
分别是直线![]() ,
,![]() 上任意两点,在直线
上任意两点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() ,在直线
,在直线![]() 上任取一点
上任取一点![]() ,作
,作![]() ,
,![]() 交直线
交直线![]() 于点
于点![]() .
.

(1)如图1,若点![]() 是线段
是线段![]() 上任意一点,
上任意一点,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 与
与![]() 互为补角,若
互为补角,若![]() ,请判断线段
,请判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
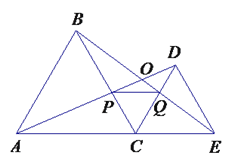
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个同心圆,大圆半径为5cm,小圆的半径为4cm,若大圆的弦AB与小圆有两个公共点,则AB的取值范围是( )
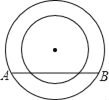
A. 4<AB<5 B. 6<AB<10 C. 6≤AB<10 D. 6<AB≤10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点P为直径BA延长线上一点,PD切⊙O于点D、过点B作BH⊥PH,点H为垂足,BH交⊙O于点C,连接BD,CD.
(1)求证:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)画出△A1B1C1沿x轴向右平移4个单位长度后得到的△A2B2C2;
(3)如果AC上有一点M(a,b)经过上述两次变换,那么对应A2C2上的点M2的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
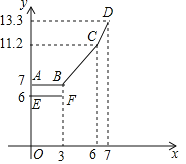
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
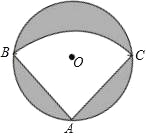
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com