
【题目】如图,点![]() 、
、![]() 分别在梯形
分别在梯形![]() 的两腰
的两腰![]() 、
、![]() 上,且
上,且![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的值为( )
的值为( )

A. 15.6 B. 15 C. 19 D. 无法计算
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
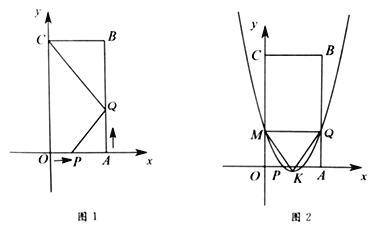
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 的同侧有两个点
的同侧有两个点![]() 、
、![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使
,使![]() 点到
点到![]() 、
、![]() 两点的距离之和最短的问题,可以通过轴对称来确定,即作出其中一点关于直线
两点的距离之和最短的问题,可以通过轴对称来确定,即作出其中一点关于直线![]() 的对称点,对称点与另一点的连线与直线
的对称点,对称点与另一点的连线与直线![]() 的交点就是所要找的点,通过这种方法可以求解很多问题.
的交点就是所要找的点,通过这种方法可以求解很多问题.
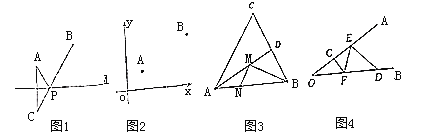
(1)如图2,在平面直角坐标系内,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值;
的最小值;
(2)如图3,在锐角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值为______.
的最小值为______.
(3)如图4,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是射线
分别是射线![]() ,
,![]() 上的动点,则
上的动点,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
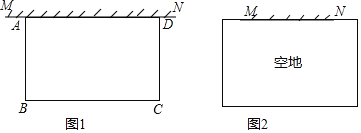
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果生产基地销售苹果,提供两种购买方式供客户选择
方式![]() :若客户缴纳
:若客户缴纳![]() 元会费加盟为生产基地合作单位,则苹果成交价为
元会费加盟为生产基地合作单位,则苹果成交价为![]() 元
元![]() 千克.
千克.
方式![]() :若客户购买数量达到或超过
:若客户购买数量达到或超过![]() 千克,则成交价为
千克,则成交价为![]() 元
元![]() 千克;若客户购买数量不足
千克;若客户购买数量不足![]() 千克,则成交价为
千克,则成交价为![]() 元
元![]() 千克.设客户购买苹果数量为
千克.设客户购买苹果数量为![]() (千克),所需费用为
(千克),所需费用为![]() (元).
(元).
(1)若客户按方式![]() 购买,请写出
购买,请写出![]() (元)与
(元)与![]() (千克)之间的函数表达式;(备注:按方式购买苹果所需费用
(千克)之间的函数表达式;(备注:按方式购买苹果所需费用![]() 生产基地合作单位会费
生产基地合作单位会费![]() 苹果成交总价)
苹果成交总价)
(2)如果购买数量超过![]() 千克,请说明客户选择哪种购买方式更省钱;
千克,请说明客户选择哪种购买方式更省钱;
(3)若客户甲采用方式![]() 购买,客户乙采用方式
购买,客户乙采用方式![]() 购买,甲、乙共购买苹果
购买,甲、乙共购买苹果![]() 千克,总费用共计
千克,总费用共计![]() 元,则客户甲购买了多少千克苹果?
元,则客户甲购买了多少千克苹果?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘被等分成六个扇形区域,并在上面依次写上数字:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .转盘指针的位置固定,转动转盘后任其自由停止.
.转盘指针的位置固定,转动转盘后任其自由停止.
![]() 当停止转动时,指针指向奇数区域的概率是多少?
当停止转动时,指针指向奇数区域的概率是多少?
![]() 请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为
请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为![]() ,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)
,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com