
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
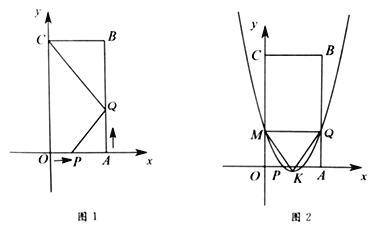
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
【答案】(1)![]() 的中点坐标是
的中点坐标是![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() .
.
【解析】(1)先根据时间t=2,和速度可得动点P和Q的路程OP和AQ的长,再根据中点坐标公式可得结论;
(2)根据矩形的性质得:∠B=∠PAQ=90°,所以当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,![]() ,②当△PAQ∽△CBQ时,
,②当△PAQ∽△CBQ时,![]() ,分别列方程可得t的值;
,分别列方程可得t的值;
(3)根据t=1求抛物线的解析式,根据Q(3,2),M(0,2),可得MQ∥x轴,∴KM=KQ,KE⊥MQ,画出符合条件的点D,证明△KEQ∽△QMH,列比例式可得点D的坐标,同理根据对称可得另一个点D.
(1)如图1,∵点A的坐标为(3,0),
∴OA=3,
当t=2时,OP=t=2,AQ=2t=4,
∴P(2,0),Q(3,4),
∴线段PQ的中点坐标为:(![]() ,
,![]() ),即(
),即(![]() ,2);
,2);
故答案为:(![]() ,2);
,2);
(2)如图1,∵四边形OABC是矩形,
∴∠B=∠PAQ=90°
∴当△CBQ与△PAQ相似时,存在两种情况:
①当△PAQ∽△QBC时,![]() ,
,
∴![]() ,
,
4t2-15t+9=0,
(t-3)(t-![]() )=0,
)=0,
t1=3(舍),t2=![]() ,
,
②当△PAQ∽△CBQ时,![]() ,
,
∴![]() ,
,
t2-9t+9=0,
t=![]() ,
,
∵0≤t≤6,![]() >7,
>7,
∴x=![]() 不符合题意,舍去,
不符合题意,舍去,
综上所述,当△CBQ与△PAQ相似时,t的值是![]() 或
或![]() ;
;
(3)当t=1时,P(1,0),Q(3,2),
把P(1,0),Q(3,2)代入抛物线y=x2+bx+c中得:
![]() ,解得:
,解得:![]() ,
,
∴抛物线:y=x2-3x+2=(x-![]() )2-
)2-![]() ,
,
∴顶点k(![]() ,-
,-![]() ),
),
∵Q(3,2),M(0,2),
∴MQ∥x轴,
作抛物线对称轴,交MQ于E,
∴KM=KQ,KE⊥MQ,
∴∠MKE=∠QKE=![]() ∠MKQ,
∠MKQ,
如图2,∠MQD=![]() ∠MKQ=∠QKE,设DQ交y轴于H,
∠MKQ=∠QKE,设DQ交y轴于H,

∵∠HMQ=∠QEK=90°,
∴△KEQ∽△QMH,
∴![]() ,
,
∴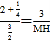 ,
,
∴MH=2,
∴H(0,4),
易得HQ的解析式为:y=-![]() x+4,
x+4,
则 ,
,
x2-3x+2=-![]() x+4,
x+4,
解得:x1=3(舍),x2=-![]() ,
,
∴D(-![]() ,
,![]() );
);
同理,在M的下方,y轴上存在点H,如图3,使∠HQM=![]() ∠MKQ=∠QKE,
∠MKQ=∠QKE,

由对称性得:H(0,0),
易得OQ的解析式:y=![]() x,
x,
则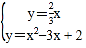 ,
,
x2-3x+2=![]() x,
x,
解得:x1=3(舍),x2=![]() ,
,
∴D(![]() ,
,![]() );
);
综上所述,点D的坐标为:D(-![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
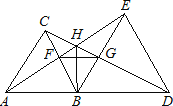
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=--![]() x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:我们可以将任意三位数记为![]() ,(其中
,(其中![]() 、
、![]() 、
、![]() 分别表示该数的百位数字,十位数字和个位数字,且
分别表示该数的百位数字,十位数字和个位数字,且![]() ),显然
),显然![]() .
.
材料二:若一个三位数的百位数字,十位数字和个位数字均不为0,则称之为初始数,比如123就是一个初始数,将初始数的三个数位上的数字交换顺序,可产生出5个新的初始数,比如由123可以产生出132,213,231,312,321这5个新初始数,这6个初始数的和成为终止数.
(1)求初始数125生成的终止数;
(2)若一个初始数![]() ,满足
,满足![]() ,且
,且![]() ,记
,记![]() ,
,![]() ,
,![]() ,若
,若![]() ,求满足条件的初始数的值.
,求满足条件的初始数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,图形ABCD是由两个二次函数y1=kx2+m(k<0)与y2=ax2+b(a>0)的部分图象围成的封闭图形.已知A(1,0)、B(0,1)、D(0,﹣3).

(1)直接写出这两个二次函数的表达式;
(2)判断图形ABCD是否存在内接正方形(正方形的四个顶点在图形ABCD上),并说明理由;
(3)如图2,连接BC,CD,AD,在坐标平面内,求使得△BDC与△ADE相似(其中点C与点E是对应顶点)的点E的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年是全面建成小康社会收官之年,某扶贫帮扶小组积极响应,对农民实施精准扶贫.某农户老张家种植花椒和黑木耳两种干货共800千克,扶贫小组通过市场调研发现,花椒市场价60元/千克,黑木耳市场价48元/千克,老张全部售完可以收入4.2万元.已知老张种植花椒成本需25元/千克,种植木耳成本需35元/千克,根据脱贫目标任务要求,老张种植花椒和黑木耳的两种干货的纯收入(销售收入-种植成本)在2万元以上才可以顺利脱贫.请你分析一下扶贫帮扶小组是否能帮助老张顺利脱贫.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com