
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

【答案】(1)解析式为y=﹣x2+6x﹣5,对称轴:直线x=3,顶点坐标(3,4);(2)k=![]() 或k=
或k=![]() ;(3)当x=2时,SPMN最大,最大值为8,此时P(2,3);(4)①当x≤1或3≤x≤5时y随x的增大而增大;②当
;(3)当x=2时,SPMN最大,最大值为8,此时P(2,3);(4)①当x≤1或3≤x≤5时y随x的增大而增大;②当![]() <k<1时,直线l与图象L2有四个交点.
<k<1时,直线l与图象L2有四个交点.
【解析】
(1)根据待定系数法,可得函数解析式;(2)根据线段的比,可得直线与x轴的交点,根据自变量与函数值的对应关系,可得答案;(3)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PH,根据三角形的面积,可得二次函数,根据二次函数的性质,可得答案;(4)①根据函数图象的增减趋势,可得答案;②根据函数图象的交点,可得直线经过D,B点,根据自变量与函数值的对应关系,可得相应的k值,可得答案.
(1)∵抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)
∴y=﹣(x﹣1)(x﹣5)=﹣(x﹣3)2+4,
∴抛物线L1的解析式为y=﹣x2+6x﹣5
对称轴:直线x=3
顶点坐标(3,4);
(2)∵直线l将线段AB分成1:3两部分,则l经过点(2,0)或(4,0),
∴0=2k﹣5或0=4 k﹣5
∴k=![]() 或k=
或k=![]() .
.
(3)如图1
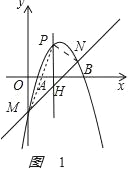 ,
,
设P(x,﹣x2+6x﹣5)是抛物线位于直线上方的一点,
解方程组![]() ,解得
,解得
![]() 或
或![]()
不妨设M(0,﹣5)、N(4,3)
∴0<x<4
过P做PH⊥x轴交直线l于点H,
则H(x,2x﹣5),
PH=﹣x2+6x﹣5﹣(2x﹣5)=﹣x2+4x,
S△PMN=![]() PHxN
PHxN
=![]() (﹣x2+4x)×4
(﹣x2+4x)×4
=﹣2(x﹣2)2+8
∵0<x<4
∴当x=2时,SPMN最大,最大值为8,此时P(2,3)
(4)如图2
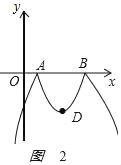 ,
,
A(1,0),B(5,0).由翻折,得D(3,﹣4),
①当x≤1或3≤x≤5时y随x的增大而增大
②当y=kx﹣5过D点时,3k﹣5=﹣4,解得k=![]() ,
,
当y=kx﹣5过B点时,5k﹣5=0,解得k=1,
直线与抛物线的交点在BD之间时有四个交点,即![]() <k<1,
<k<1,
当![]() <k<1时,直线l与图象L2有四个交点.
<k<1时,直线l与图象L2有四个交点.


科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以![]() 米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为
米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为![]() (米)与时间
(米)与时间![]() (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:

(1)填空:![]() ______;
______;![]() ______;
______;![]() ______.
______.
(2)求线段![]() 所在直线的解析式.
所在直线的解析式.
(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
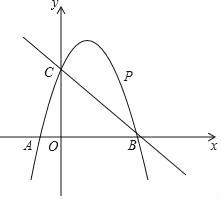
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
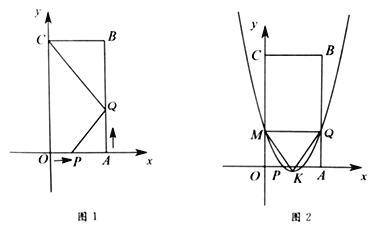
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
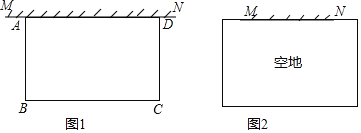
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com