Question

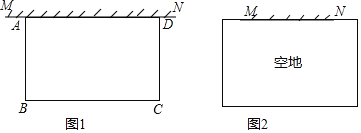
【题目】空地上有一段长为a米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，已知木栏总长为100米．

（1）已知a=20，矩形菜园的一边靠墙，另三边一共用了100米木栏，且围成的矩形菜园面积为450平方米．如图1，求所利用旧墙AD的长；

（2）已知0＜α＜50，且空地足够大，如图2．请你合理利用旧墙及所给木栏设计一个方案，使得所围成的矩形菜园ABCD的面积最大，并求面积的最大值．

Answer 1

【答案】（1）利用旧墙AD的长为10米．（2）见解析.

【解析】

（1）按题意设出AD，表示AB构成方程；

（2）根据旧墙长度a和AD长度表示矩形菜园长和宽，注意分类讨论s与菜园边长之间的数量关系．

（1）设AD=x米，则AB=米

依题意得，＝450

解得x1=10，x2=90

∵a=20，且x≤a

∴x=90舍去

∴利用旧墙AD的长为10米．

（2）设AD=x米，矩形ABCD的面积为S平方米

①如果按图一方案围成矩形菜园，依题意

得：

S=，0＜x＜a

∵0＜a＜50

∴x＜a＜50时，S随x的增大而增大

当x=a时，S最大=50a-a2

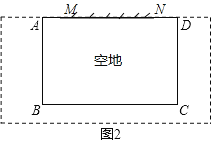
②如按图2方案围成矩形菜园，依题意得

S=，a≤x＜50+

当a＜25+＜50时，即0＜a＜时，

则x=25+时，S最大=（25+）2=，

当25+≤a，即≤a＜50时，S随x的增大而减小

∴x=a时，S最大==，

综合①②，当0＜a＜时，-（）=＞0

＞，此时，按图2方案围成矩形菜园面积最大，最大面积为平方米

当≤a＜50时，两种方案围成的矩形菜园面积最大值相等．

∴当0＜a＜时，围成长和宽均为（25+）米的矩形菜园面积最大，最大面积为平方米；

当≤a＜50时，围成长为a米，宽为（50-）米的矩形菜园面积最大，最大面积为（）平方米．