
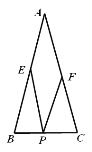
【题目】如图,在△ABC中,AB=AC=4,BC=2,点P、E、F分别为边BC、AB、AC上的任意点,则PE+PF的最小值是_____.
【答案】![]()
【解析】
当PE⊥AB,PF⊥AC时,PE+PF的值最小.
解:如图,作CG⊥AB于G,PH⊥CG于H,
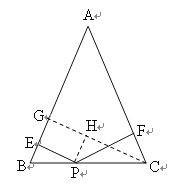
当PE⊥AB,PF⊥AC时,则∠EGH=GHP=∠PEG=90°,
∴四边形PEGH为矩形,
∴PE=HG,PH∥AB,
∴∠B=∠HPC,
∵AB=AC,
∴∠B=∠FCP,
∴∠HPC=∠FCP,
∵∠PHC=∠CFP=90°,PC=CP,
∴△PHC≌△CFP(AAS),
∴CH=PF
∴PE+PF=HG+CH=CG,
故此时PE+PF将取得最小值.
在Rt△ACG中,
∵AC=4,
∴CG2=AC2-AG2=42-AG2,
在Rt△BCG中,
∵BC=2,BG=AB-AG=4-AG,
∴CG2=BC2-BG2=22-(4-AG)2,
∴42-AG2=22-(4-AG)2,
∴AG=![]() ,
,
∴CG=![]() =
=![]() =
=![]() ,
,
∴PE+PF=![]() ,
,
即PE+PF的最小值为![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,以BC为直径的半圆O与边AB相交于点D,DE⊥AC,垂足为点E.
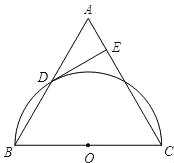
(1)判断DE与⊙O的位置关系,并证明你的结论;
(2)若AE=1,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是( )

A. 4≥x>2.4 B. 4≥x≥2.4 C. 4>x>2.4 D. 4>x≥2.4
查看答案和解析>>
科目:初中数学 来源: 题型:
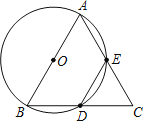
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
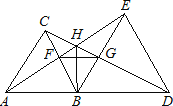
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:等腰△ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为( )
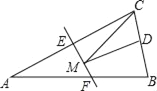
A. 6 B. 8 C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L1:y=﹣x2+bx+c经过点A(1,0)和点B(5,0)已知直线l的解析式为y=kx﹣5.
(1)求抛物线L1的解析式、对称轴和顶点坐标.
(2)若直线l将线段AB分成1:3两部分,求k的值;
(3)当k=2时,直线与抛物线交于M、N两点,点P是抛物线位于直线上方的一点,当△PMN面积最大时,求P点坐标,并求面积的最大值.
(4)将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方,将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围;
②直接写出直线l与图象L2有四个交点时k的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com