练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，正方形ABCD中，AD=12，G是BC的中点．将△ABG沿AG对折至△AFG，延长GF交DC于点E，则DE的长是_____．

    【答案】4

    【解析】

    如图，连接AE，根据翻折变换的性质和正方形的性质可证Rt△AFE≌Rt△ADE；在直角△ECG中，设DE=FE=x，然后根据勾股定理计算即可求出DE的长．

    解：如图，连接AE，

    ∵AB=AD=AF，∠D=∠AFE=90°，

    在Rt△AFE和Rt△ADE中，

    ∵

    ∴Rt△AFE≌Rt△ADE，

    ∴EF=DE.

    设DE=FE=x，则EC=12-x．

    ∵G为BC中点，BC=12，

    ∴CG=6，

    在Rt△ECG中，根据勾股定理，得：(12-x)2+36=(x+6)2，

    解得，x=4，

    则DE=4.

    故答案为4.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，是的直径，弦于点，交于点，连结、、，若．

    求证：直线为的切线；

    若，，求线段的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．

    （1）在图1中证明CE=CF；

    （2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；

    （3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（9分）如图，AB是半圆O的直径，点P是半圆上不与点A、B重合的一个动点，延长BP到点C，使PC=PB，D是AC的中点，连接PD，PO.

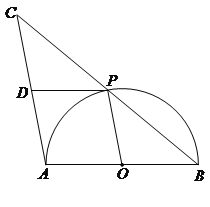
    （1）求证：△CDP≌△POB；

    （2）填空：

    ① 若AB=4，则四边形AOPD的最大面积为 ；

    ② 连接OD，当∠PBA的度数为 时，四边形BPDO是菱形.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为决定谁获得仅有的一张电影票，甲和乙设计了如下游戏：在三张完全相同的卡片上，分别写上字母，，，背面朝上，每次活动洗均匀．

    甲说：我随机抽取一张，若抽到字母，电影票归我；

    乙说：我随机抽取一张后放回，再随机抽取一张，若两次抽取的字母相同的电影票归我．

    求甲获得电影票的概率；求乙获得电影票的概率；此游戏对谁有利？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC=4，BC=2，点P、E、F分别为边BC、AB、AC上的任意点，则PE+PF的最小值是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在平面直角坐标系中，直线分别与轴，轴交于两点．

    （1）求线段AB的长度；

    （2）若点在第二象限，且△为等腰直角三角形，求点的坐标；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“有两角及其中一角的平分线对应相等的两个三角形全等”是_____命题．（填“真”或“假”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

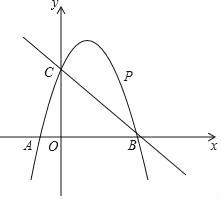
    【题目】如图，已知二次函数y=ax2+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）．点P是直线BC上方的抛物线上一动点．

    （1）求二次函数y=ax2+2x+c的表达式；

    （2）连接PO，PC，并把△POC沿y轴翻折，得到四边形POP′C．若四边形POP′C为菱形，请求出此时点P的坐标；

    （3）当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积．

    查看答案和解析>>

    同步练习册答案