
【题目】(9分)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
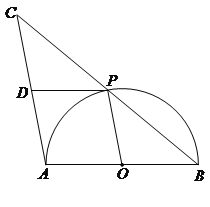
(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
【答案】(1)参见解析;(2)①4;②60º.
【解析】试题(1)利用边角边证明这两个三角形全等;(2)①当∠CAB=90时,四边形AOPD有最大面积,此时等于AO乘以AD的值;②当四边形BPDO是菱形时,可推出OB=OP=OD=DP,三角形DPO是等边三角形,所以∠PDO=60,∵菱形对角相等,∴∠PBA的度数也等于60.
试题解析:(1)∵D是AC的中点,且PC=PB,∴DP∥AB,DP=![]() AB,∴∠CPD=∠PBO,∵OB=
AB,∴∠CPD=∠PBO,∵OB=![]() AB,∴DP=OB,∴△CDP≌△POB;(2)①∵四边形AOPD是平行四边形,当高等于AD时,四边形AOPD有最大面积,此时∠CAB=90,最大面积=AO×AD=2×2=4;②当四边形BPDO是菱形时,OD=DP=OB,∵OB=OP,∴OP=OD=DP,∴△DPO是等边三角形,∴∠PDO=60,∵菱形对角相等,∴∠PBA=∠PDO=60.
AB,∴DP=OB,∴△CDP≌△POB;(2)①∵四边形AOPD是平行四边形,当高等于AD时,四边形AOPD有最大面积,此时∠CAB=90,最大面积=AO×AD=2×2=4;②当四边形BPDO是菱形时,OD=DP=OB,∵OB=OP,∴OP=OD=DP,∴△DPO是等边三角形,∴∠PDO=60,∵菱形对角相等,∴∠PBA=∠PDO=60.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊿ABC中,∠B = 50,∠C = 70,AD是高,AE是角平分线,
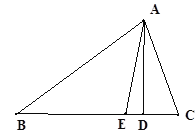
(1)∠BAC=__________,∠DAC=__________.(填度数)
(2)求∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,点M,N分别是对角线AC,BE的中点,连接MN,PM,PN,若∠DAP=60°,AP2+3PB2=2,则线段MN的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点(且点P不与点B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点.设AM的长为x,则x的取值范围是( )

A. 4≥x>2.4 B. 4≥x≥2.4 C. 4>x>2.4 D. 4>x≥2.4
查看答案和解析>>
科目:初中数学 来源: 题型:
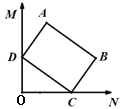
【题目】如图,∠MON=90°,矩形ABCD的顶点C、D分别在边ON,OM上滑动,AB=9,BC=6,在滑动过程中,点A到点O的最大距离为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
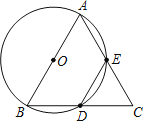
【题目】如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC、AC于点D、E,且点D为BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
(3)在线段AB的延长线上是否存在一点P,使△PBD≌△AED?若存在,请求出PB的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
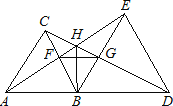
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=--![]() x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
x+8与x轴,y轴分别交于点A,点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求AB的长和点C的坐标;
(2)求直线CD的表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com