
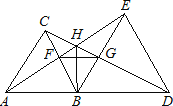
【题目】.如图所示,已知△ABC和△BDE都是等边三角形,下列结论:①AE=CD;②BF=BG;③BH平分∠AHD;④∠AHC=60°;⑤△BFG是等边三角形;⑥FG∥AD,其中正确的有( )
A. 3个 B. 4个 C. 5个 D. 6个
【答案】D
【解析】∵△ABC与△BDE为等边三角形,
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
即AB=BC,BD=BE,∠ABE=∠CBD
∴△ABE≌△CBD,
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴△BGD≌△BFE,
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
∵BF=BG,AB=BC,∠ABF=∠CBG=60°,
∴△ABF≌△CGB,
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∵∠FHG+∠FBG=120°+60°=180°,
∴B、G、H、F四点共圆,
∵FB=GB,
∴∠FHB=∠GHB,
∴BH平分∠GHF,
∴题中①②③④⑤⑥都正确.
故选D.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
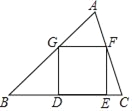
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
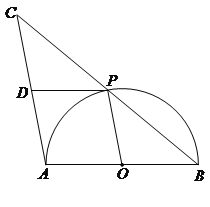
(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
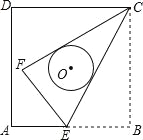
【题目】如图,正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位长度的速度向点
以每秒2个单位长度的速度向点![]() 运动,当点
运动,当点![]() 与点
与点![]() 重合时运动停止.设运动时间为
重合时运动停止.设运动时间为![]() 秒.
秒.
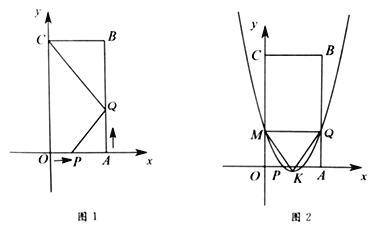
(1)当![]() 时,线段
时,线段![]() 的中点坐标为________;
的中点坐标为________;
(2)当![]() 与
与![]() 相似时,求
相似时,求![]() 的值;
的值;
(3)当![]() 时,抛物线
时,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,如图2所示.问该抛物线上是否存在点
,如图2所示.问该抛物线上是否存在点![]() ,使
,使![]() ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com