
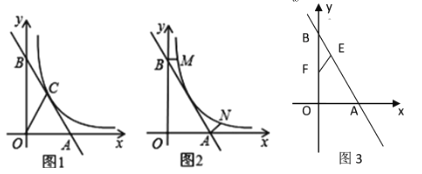
【题目】如图1,一次函数y=2x+4的图象交x轴于点A,交y轴于点B,与反比例函数y=![]() (x>0)的图象交于点C,连OC,若S△AOC=2.
(x>0)的图象交于点C,连OC,若S△AOC=2.
(1)求反比例函数的解析式;
(2)如图3,点E, F分别是线段AB和线段OB上的动点,点E从点B出发,沿线段BA运动,点F从点O出发,沿线段OB运动,速度都是每秒1个单位长度。运动时间为t秒,当其中一点到达终点后,另一点也随之停止运动.是否存在某个时刻。使得△BEF是直角三角形?若存在,求出t的值若不存在,请说明理由:
(3)如图2,过点B作BM⊥OB交反比例函数y=![]() (x>0)的图象于点M,点N为反比例函数 y=
(x>0)的图象于点M,点N为反比例函数 y=![]() (x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
(x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
【答案】(1)y=![]() (2)存在某个时刻,使得△BEF是直角三角形,此时t=20-8
(2)存在某个时刻,使得△BEF是直角三角形,此时t=20-8![]() 或8
或8![]() -16 (3)y=
-16 (3)y=![]()
【解析】
(1)先由一次函数的解析式为y=-2x+4及x轴、y轴上点的坐标特征,求出A(2,0),B(0,4),再根据S△AOC=2,利用三角形的面积公式求出C(1,2),然后运用待定系数法即可求出反比例函数的解析式;
(2)根据题意可得:OF=t,BF=4-t,BE=t,当△BEF是直角三角形时,有两种情况,∠BFE=90![]() 或∠BEF=90
或∠BEF=90![]() ,再根据两角相等证明△BEF与△BOA相似,列方程即可求出t的值
,再根据两角相等证明△BEF与△BOA相似,列方程即可求出t的值
(3)由A(2,0),B(0,4),C(1,2)三点的坐标,可知C为AB的中点,如图2,延长BM交AN的延长线于D,根据等角对等边得到DB=DA,再连结DC,由等腰三角形三线合一的性质得出DC⊥BA,则∠DCB=∠BOA=90°,由平行线的性质易得∠DBA=∠BAO,那么△DBC∽△BAO,得出DB:BC=BA:AO,求出DB=5,得到D(5,4),然后运用待定系数法即可求出直线AN的解析式;
:

(1)∵一次函数y=-2x+4的图象交x轴于点A,交y轴于点B,
∴A(2,0),B(0,4).
设C(m,n).
∵S△AOC=2,
∴![]() ×2×n=2,
×2×n=2,
解得n=2.
又n=-2m+4,
∴m=1,
∴C(1,2),
所以反比例函数的解析式为y=![]() ;
;
(2)根据题意可得:OF=t,BF=4-t,BE=t,(0![]() )
)
在Rt△ABO中,∵A(2,0),B(0,4)则AB==2![]()
当△BEF是直角三角形时,有两种情况,
①当∠BFE=90![]() 时,
时,
∴∠BFE=∠AOB ∵∠EBF=∠ABO
∴△BEF![]() △BAO
△BAO
∴![]()
∴![]()
∴t=20-8![]()
②当∠BEF=90![]() 时
时
同理可得△BEF![]() △BOA
△BOA
∴![]()
∴![]()
∴t=8![]() -16
-16
综上所述,存在某个时刻,使得△BEF是直角三角形,此时t=20-8![]()
或8![]() -16
-16
(3)∵A(2,0),B(0,4),C(1,2),
∴C为AB的中点,AO=2,BO=4,AB=2![]() ,
,
∴BC=![]() .
.
如图2,延长BM交AN的延长线于D,
∵∠ABM=∠BAN,
∴DB=DA,
连结DC,则DC⊥BA,
∵BM⊥OB,
∴BM∥OA,
∴∠DBA=∠BAO,
又∠DCB=∠BOA=90°,
∴△DBC∽△BAO,
∴DB:BC=BA:AO,
∴DB=5,
∴D(5,4).
设直线AN的解析式为y=mx+b,
∵直线AN过A(2,0)、D(5,4),
∴![]() ,解得
,解得
∴直线AN的解析式为y=![]() ;
;


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④S四边形CDEF=![]() S△ABF,其中正确的结论有________个。
S△ABF,其中正确的结论有________个。

查看答案和解析>>
科目:初中数学 来源: 题型:
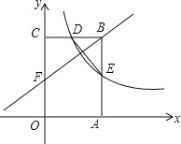
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),反比例函数y=![]() (k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(k>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求反比例函数的表达式及点E的坐标;
(2)点F是OC边上一点,若△FBC∽△DEB,求点F的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(满分12分)在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点
轴的两个交点
分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写:![]() = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ;
(2)在![]() 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.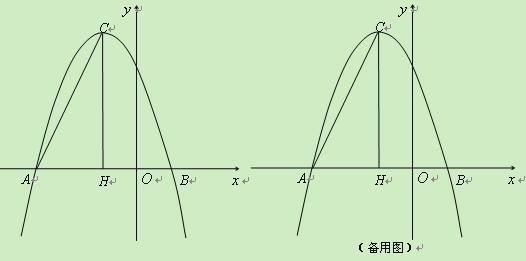
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
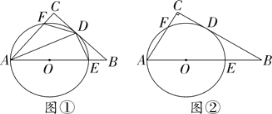
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com