练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是⊙O的直径，且经过弦CD的中点H，已知sin∠CDB=，BD=5，则AH的长为（　　）

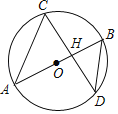
    A. B. C. D.

    【答案】B

    【解析】连接OD，由垂径定理得出AB⊥CD，由三角函数求出BH=3，由勾股定理得出DH==4，设OH=x，则OD=OB=x+3，在Rt△ODH中，由勾股定理得出方程，解方程即可．

    连接OD，如图所示：

    ∵AB是⊙O的直径，且经过弦CD的中点H，

    ∴AB⊥CD，

    ∴∠OHD=∠BHD=90°，

    ∵sin∠CDB=，BD=5，

    ∴BH=3，

    ∴DH==4，

    设OH=x，则OD=OB=x+3，

    在Rt△ODH中，由勾股定理得：x2+42=（x+3）2，

    解得：x=，

    ∴OH=，

    ∴AH=OA+OH=+3+=，

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC 中，∠ABC 和∠ACB 的角平分线交于点 M．

    （1）若∠ABC=40°，∠ACB=60°，求∠BMC 的度数；

    （2）∠BMC 可能是直角吗？作出判断，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，DE是边AB的垂直平分线，交AB于E、交AC于D，连接BD．

    （1）若∠ABC＝∠C，∠A＝40°，求∠DBC的度数；

    （2）若AB＝AC，且△BCD的周长为18cm，△ABC的周长为30cm，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

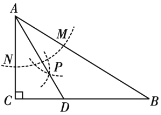
    【题目】如图，在中，，以为圆心，任意长为半径画弧分别交于点和，再分别以点为圆心，大于的长为半径画弧，两弧交于点，连接并延长交于点，则下列说法①平分；②；③点在的垂直平分线上；④连接，则，其中正确的是__________．（填序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

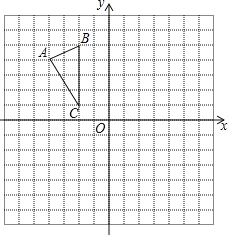
    【题目】如图，△ABC在平面直角坐标系内，顶点的坐标分别为A（﹣4，4），B（﹣2，5），C（﹣2，1）．

    （1）平移△ABC，使点C移到点C1（﹣2，﹣4），画出平移后的△A1B1C1，并写出点A1，B1的坐标；

    （2）将△ABC绕点（0，3）旋转180°，得到△A2B2C2，画出旋转后的△A2B2C2；

    （3）求（2）中的点C旋转到点C2时，点C经过的路径长（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．

    （1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．

    （2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．

    （3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC、BD相交于点O，AB=CD，AC=BD.求证：(1) ∠ABD=∠DCA；(2) AO=DO.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若 ( x 2 px )( x 2 3x q) 的积中不含 x 项与 x3 项

    （1）求 p、q 的值；（2）求代数式（-2p2q）2+（3pq）-1+p2013q2014的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某社区计划对面积为3600m2的区域进行绿化，经投标，由甲，乙两个工程队来完成,已知甲队4天能完成绿化的面积等于乙队8天完成绿化的面积，甲队3天能完成绿化的面积比乙队5天能完成绿化面积多50m2

    (1)求甲、乙两工程队每天能完成绿化的面积；

    (2)若甲队每天化费用是1.2万元，乙队每天绿化费用为0.5万元，要使这次绿化的总费用不超过40万元，则至少应安排乙工程队绿化多少天？

    查看答案和解析>>

    同步练习册答案