
【题目】(满分12分)在平面直角坐标系中,抛物线![]() 与
与![]() 轴的两个交点
轴的两个交点
分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写:![]() = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ;
(2)在![]() 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.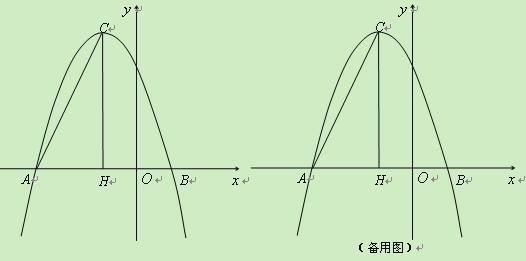
【答案】解:(1)![]() ,顶点C的坐标为(-1,4)………………………… 3分
,顶点C的坐标为(-1,4)………………………… 3分
(2)假设在y轴上存在满足条件的点D, 过点C作CE⊥y轴于点E.
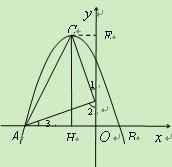
![]() 由∠CDA=90°得,∠1+∠2="90°. " 又∠2+∠3=90°,
由∠CDA=90°得,∠1+∠2="90°. " 又∠2+∠3=90°,
∴∠3=∠1. 又∵∠CED=∠DOA =90°,
![]() ∴△CED∽△DOA,∴
∴△CED∽△DOA,∴![]() .
.
![]()
![]()
![]()
![]() 设D(0,c),则
设D(0,c),则![]() .
.
变形得![]() ,解之得
,解之得![]() .
.
综合上述:在y轴上存在点D(0,3)或(0,1),
使△ACD是以AC为斜边的直角三角形. ………………………………… 7分
(3)①若点P在对称轴右侧(如图①),只能是△PCQ∽△CAH,得∠QCP=∠CAH.
延长CP交x轴于M,
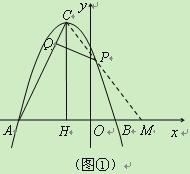
∴AM=CM, ∴AM2=CM2.
设M(m,0),则( m+3)2=42+(m+1)2,∴m=2,即M(2,0).
设直线CM的解析式为y=k1x+b1,
则![]() , 解之得
, 解之得![]() ,
,![]() .
.
∴直线CM的解析式![]() .…………………………………………… 8分
.…………………………………………… 8分
联立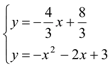 ,解之得
,解之得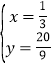 或
或![]() (舍去).∴
(舍去).∴![]() .…… 9分
.…… 9分
②若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.
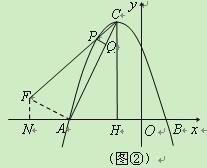
由△CFA∽△CAH得![]() ,
,
由△FNA∽△AHC得![]() .
.
∴![]() , 点F坐标为(-5,1). …………………………………10分
, 点F坐标为(-5,1). …………………………………10分
设直线CF的解析式为y=k2x+b2,则![]() ,解之得
,解之得![]() .
.
∴直线CF的解析式![]() . ……………………………………………11分
. ……………………………………………11分
联立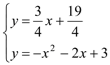 ,解之得
,解之得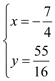 或
或![]() (舍去). ∴
(舍去). ∴![]() .
.
∴满足条件的点P坐标为![]() 或
或![]() ………………………………12分
………………………………12分
【解析】
略


科目:初中数学 来源: 题型:
【题目】下列方程中,是一元二次方程共有( )
①x2﹣![]() +3=0;②2x2﹣3xy+4=0; ③x2﹣4x+k=0;④x2+mx﹣1=0;⑤3x2+x=20.
+3=0;②2x2﹣3xy+4=0; ③x2﹣4x+k=0;④x2+mx﹣1=0;⑤3x2+x=20.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场学校积极开展阳光体育活动,组织了九年级学生定点投篮,规定每人投篮3次.现对九年级(1)班每名学生投中的次数进行统计,绘制成如下的两幅统计图,根据图中提供的信息,回答下列问题.
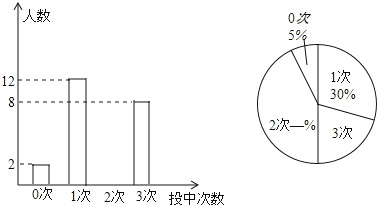
(1)求出九年级(1)班学生人数;
(2)补全两个统计图;
(3)求出扇形统计图中3次的圆心角的度数;
(4)若九年级有学生200人,估计投中次数在2次以上(包括2次)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
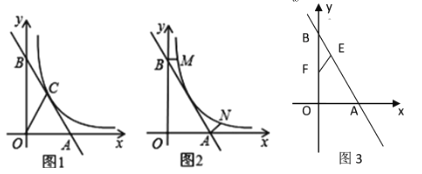
【题目】如图1,一次函数y=2x+4的图象交x轴于点A,交y轴于点B,与反比例函数y=![]() (x>0)的图象交于点C,连OC,若S△AOC=2.
(x>0)的图象交于点C,连OC,若S△AOC=2.
(1)求反比例函数的解析式;
(2)如图3,点E, F分别是线段AB和线段OB上的动点,点E从点B出发,沿线段BA运动,点F从点O出发,沿线段OB运动,速度都是每秒1个单位长度。运动时间为t秒,当其中一点到达终点后,另一点也随之停止运动.是否存在某个时刻。使得△BEF是直角三角形?若存在,求出t的值若不存在,请说明理由:
(3)如图2,过点B作BM⊥OB交反比例函数y=![]() (x>0)的图象于点M,点N为反比例函数 y=
(x>0)的图象于点M,点N为反比例函数 y=![]() (x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
(x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠ACB=90°,AC=BC=4,M为AB中点,D是射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,则点D在运动过程中ME的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各式因式分解
(1)2a3b﹣8ab3
(2)﹣x3+x2y﹣![]() xy2
xy2
(3)(7x2+2y2)2﹣(2x2+7y2)2
(4)(x2+4x)2+(x2+4x)﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A、B 两点,交 y 轴于 C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论:①abc>0;②4a﹣2b+c>0;③5a+2c>3b;④(4a﹣b)(2a+b)<0;正确的有( )个.
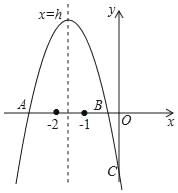
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com