【题目】下列方程中，是一元二次方程共有( )
①x2﹣
+3=0；②2x2﹣3xy+4=0； ③x2﹣4x+k=0；④x2+mx﹣1=0；⑤3x2+x=20．
A. 2个 B. 3个 C. 4个 D. 5个
新非凡教辅冲刺100分系列答案科目：初中数学 来源： 题型：
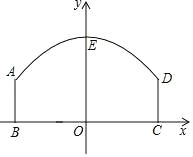
【题目】如图，一隧道的横截面是由一段抛物线及矩形的三边围成的，隧道宽BC＝10米，矩形部分高AB＝3米，抛物线型的最高点E离地面OE＝6米，按如图建立一个以BC为x轴，OE为y轴的直角坐标系．
（1）求抛物线的解析式；
（2）如果该隧道内设有双车道，现有一辆货运卡车高4.5米，宽3米，这辆货运卡车能顺利通过隧道吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，对于点P（a，b）和点Q（a，b′），给出如下定义：
若b′=
，则称点Q为点P的理想点．例如：点（1，2）的理想点的坐标是（1，﹣2），点（﹣2，3）的理想点的坐标是（﹣2，3）．
（1）点（
，﹣1）理想点的坐标是_____；若点C在函数y=2x2的图象上，则它的理想点是A（1，﹣2），B（﹣1，2）中的哪一个？_____；
（2）若点P在函数y=﹣2x+4（﹣2≤x≤k，k＞﹣2）的图象上，其理想点为Q：
①若其理想点Q的纵坐标b′的取值范围是﹣6≤b′≤10，求k的值；
②在①的条件下，若点P的理想点Q都不在反比例函数y=
（m＜0，x＞0）上，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图所示的正方形网格中，每个网格的单位长度为1，△ABC的顶点均在格点上，根据所给的平面直角坐标系解答下列问题：
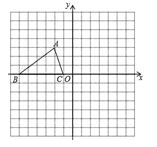
（1）A点的坐标为________；B点的坐标为________；C点的坐标为________．
（2）将点A、B、C的横坐标保持不变，纵坐标分别乘以-1，分别得点A'、B'、C'，并连接A'、B'、C'得△A' B' C'，请画出△A' B' C'．
（3）△A' B' C'与△ABC的位置关系是________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，阳光通过窗口照到教室内，竖直窗框在地面上留下2.1 m长的影子如图所示，已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m，窗口底边离地面的距离BC=1.2 m，试求窗口的高度（即AB的值）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，放在直角坐标系中的正方形ABCD边长为4，现做如下实验：抛掷一枚均匀的正四面体骰子（它有四个顶点，各顶点的点数分别是1至4这四个数字中一个），每个顶点朝上的机会是相同的，连续抛掷两次，将骰子朝上的顶点数作为直角坐标中P点的坐标）第一次的点数作横坐标，第二次的点数作纵坐标）．
（1）求P点落在正方形ABCD面上（含正方形内部和边界）的概率．
（2）将正方形ABCD平移整数个单位，则是否存在一种平移，使点P落在正方形ABCD
面上的概率为0.75；若存在，指出其中的一种平移方式；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC于点F，连接DF，分析下列五个结论：①△AEF∽△CAB；②CF=2AF；③DF=DC；④S四边形CDEF=
S△ABF，其中正确的结论有________个。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（满分12分）在平面直角坐标系中，抛物线
与
轴的两个交点
分别为A（-3，0）、B（1，0），过顶点C作CH⊥x轴于点H.
（1）直接填写：
= ，b= ，顶点C的坐标为 ；
（2）在
轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标.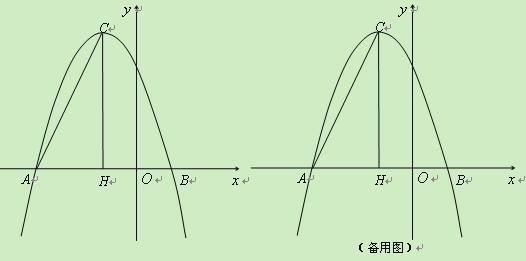
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
