
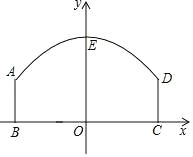
【题目】如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.
(1)求抛物线的解析式;
(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本是每千克30元,规定每千克售价不低于成本,且不高于90元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,当售价每千克50元时,销售量y为80千克;当售价每千克60元时,销售量y为60千克;
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
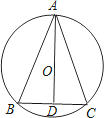
【题目】如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+1)x+![]() (m2+1)=0有两个相等的实数根.
(m2+1)=0有两个相等的实数根.
(1)求m的值;
(2)将y=﹣x2+(m+1)x﹣![]() (m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(3)在(2)的条件下,当直线y=2x+n与变化后的图象有公共点时,求n2﹣4n的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波某公司经销一种绿茶,每千克成本为![]() 元.市场调查发现,在一段时间内,销售量
元.市场调查发现,在一段时间内,销售量![]() (千克)随销售单价
(千克)随销售单价![]() (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为:![]() .设这种绿茶在这段时间内的销售利润为
.设这种绿茶在这段时间内的销售利润为![]() (元),解答下列问题:
(元),解答下列问题:
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售单价![]() 取何值时,销售利润
取何值时,销售利润![]() 的值最大,最大值为多少?
的值最大,最大值为多少?
(3)如果物价部门规定这种绿茶的销售单价不得高于![]() 元/千克,公司想要在这段时间内获得
元/千克,公司想要在这段时间内获得![]() 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中,是一元二次方程共有( )
①x2﹣![]() +3=0;②2x2﹣3xy+4=0; ③x2﹣4x+k=0;④x2+mx﹣1=0;⑤3x2+x=20.
+3=0;②2x2﹣3xy+4=0; ③x2﹣4x+k=0;④x2+mx﹣1=0;⑤3x2+x=20.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com