
【题目】某超市销售一种商品,成本是每千克30元,规定每千克售价不低于成本,且不高于90元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,当售价每千克50元时,销售量y为80千克;当售价每千克60元时,销售量y为60千克;
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
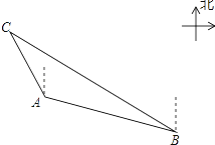
【题目】如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援,要求马上前去救援.此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里,则A、C两地之间的距离为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一张矩形纸片,长10cm,宽6cm,在它的四角各减去一个同样的小正方形,然后折叠成一个无盖的长方体纸盒.若纸盒的底面(图中阴影部分)面积是32cm2,求剪去的小正方形的边长.设剪去的小正方形边长是xcm,根据题意可列方程为( )

A. 10×6﹣4×6x=32 B. (10﹣2x)(6﹣2x)=32
C. (10﹣x)(6﹣x)=32 D. 10×6﹣4x2=32
查看答案和解析>>
科目:初中数学 来源: 题型:
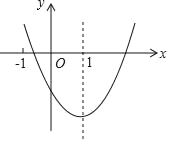
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论①abc>0;②b2﹣4ac<0;③a+b+c<0;④2a+b=0.其中正确的是( )
A. ①②③ B. ②④ C. ②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某校为了解九年级男同学的体育考试准备情况,随机抽取部分男同学进行了1000米跑测试.按照成绩分为优秀、良好、合格与不合格四个等级.学校绘制了如下不完整的统计图.
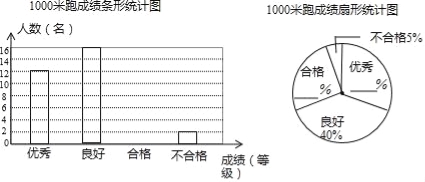
(1)根据给出的信息,补全两幅统计图;
(2)该校九年级有600名男生,请估计成绩未达到良好有多少名?
(3)某班甲、乙两位成绩优秀的同学被选中参加即将举行的学校运动会1000米比赛,预赛分为A、B、C三组进行,选手由抽签确定分组.甲、乙两人恰好分在同一组的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
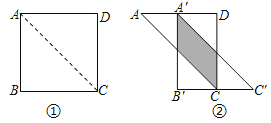
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为0.5cm2,则它移动的距离AA′等于( )
A.![]() cmB.
cmB.![]() cmC.
cmC.![]() cm或
cm或![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
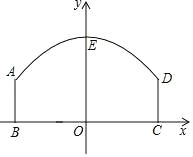
【题目】如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.
(1)求抛物线的解析式;
(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
若b′=![]() ,则称点Q为点P的理想点.例如:点(1,2)的理想点的坐标是(1,﹣2),点(﹣2,3)的理想点的坐标是(﹣2,3).
,则称点Q为点P的理想点.例如:点(1,2)的理想点的坐标是(1,﹣2),点(﹣2,3)的理想点的坐标是(﹣2,3).
(1)点(![]() ,﹣1)理想点的坐标是_____;若点C在函数y=2x2的图象上,则它的理想点是A(1,﹣2),B(﹣1,2)中的哪一个?_____;
,﹣1)理想点的坐标是_____;若点C在函数y=2x2的图象上,则它的理想点是A(1,﹣2),B(﹣1,2)中的哪一个?_____;
(2)若点P在函数y=﹣2x+4(﹣2≤x≤k,k>﹣2)的图象上,其理想点为Q:
①若其理想点Q的纵坐标b′的取值范围是﹣6≤b′≤10,求k的值;
②在①的条件下,若点P的理想点Q都不在反比例函数y=![]() (m<0,x>0)上,求m的取值范围.
(m<0,x>0)上,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com