
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论①abc>0;②b2﹣4ac<0;③a+b+c<0;④2a+b=0.其中正确的是( )
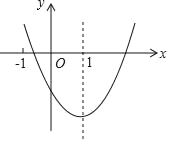
A. ①②③ B. ②④ C. ②③ D. ①③④
【答案】D
【解析】
①由二次函数图象的开口、对称轴及与y轴交点的位置,即可得出a>0,b=-2a<0,c<0,进而可得出abc>0,结论①正确;②由二次函数图象与x轴有两个交点,可得出b2-4ac>0,结论②错误;③由当x=1时y<0,可得出a+b+c<0,结论③正确;④由b=-2a,可得出2a+b=0,结论④正确.综上即可得出结论.
①∵二次函数图象开口向上,对称轴为直线x=1,与y轴交于负半轴,
∴a>0,-![]() =1,c<0,
=1,c<0,
∴b=-2a<0,
∴abc>0,结论①正确;
②∵二次函数图象与x轴有两个交点,
∴b2-4ac>0,结论②错误;
③∵当x=1时,y<0,
∴a+b+c<0,结论③正确;
④∵b=-2a,
∴2a+b=0,结论④正确.
综上所述:正确的结论有①③④.
故选D.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
(1)求k的取值范围;
(2)若k为大于3的整数,且该方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本是每千克30元,规定每千克售价不低于成本,且不高于90元.经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,当售价每千克50元时,销售量y为80千克;当售价每千克60元时,销售量y为60千克;
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入﹣成本),并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
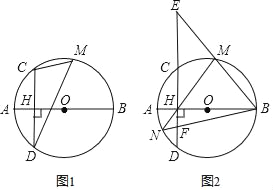
【题目】如图1,线段AB是圆O的直径,弦CD⊥AB于点H,点M是弧CBD上任意一点,AH=4,CD=16.
(1)求圆O的半径r的长度;
(2)求tan∠CMD;
(3)如图2,直径BM交直线CD于点E,直线MH交圆O于点N,连接BN交CE于点F,求HEHF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+1)x+![]() (m2+1)=0有两个相等的实数根.
(m2+1)=0有两个相等的实数根.
(1)求m的值;
(2)将y=﹣x2+(m+1)x﹣![]() (m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(3)在(2)的条件下,当直线y=2x+n与变化后的图象有公共点时,求n2﹣4n的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
新定义:
将一个平面图形分为面积相等的两部分的直线叫做该平面图形的“等积线”,其“等积线”被该平面图形截得的线段叫做该平面图形的“等积线段”(例如圆的直径就是圆的“等积线段”)
解决问题:
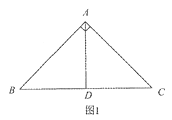
已知在Rt△ABC中,∠BAC=90°,AB=AC=2![]() .
.
(1)如图1,若AD⊥BC,垂足为D,则AD是△ABC的一条等积线段,直接写出AD的长;
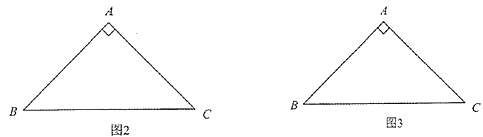
(2)在图2和图3中,分别画出一条等积线段,并直接写出它们的长度. (要求:图1、图2和图3中的等积线段的长度各不相等)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com