【题目】已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
（1）求k的取值范围；
（2）若k为大于3的整数，且该方程的根都是整数，求k的值．
科目：初中数学 来源： 题型：
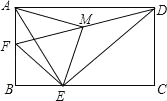
【题目】如图，在矩形ABCD中，AB=4，AD=6，点F是AB的中点，E为BC边上一点，且EF⊥ED，连结DF，M为DF的中点，连结MA，ME．若AM⊥ME，则AE的长为（ ）
A．5 B．2
C．2
D．4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（2017浙江省宁波市）在一次课题学习中，老师让同学们合作编题，某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解：
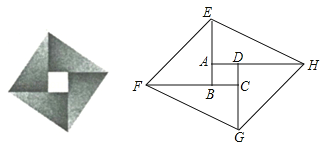
如图，将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H，使得AE=CG，BF=DH，连接EF，FG，GH，HE．
（1）求证：四边形EFGH为平行四边形；
（2）若矩形ABCD是边长为1的正方形，且∠FEB=45°，tan∠AEH=2，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】公园里有甲、乙两组游客正在做团体游戏，两组游客的年龄如下：（单位：岁）
甲组：13，13，14，15，15，15，15，16，17，17；
乙组：3，4，4，5，5，6，6，6，54，57．
我们很想了解一下甲、乙两组游客的年龄特征，请你运用“数据的代表”的有关知识对甲、乙两组数据进行分析，帮我们解决这个问题．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：
①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，
其中结论正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论：①抛物线的开口向下；②其图象的对称轴为x=1；③当x＜1时，函数值y随x的增大而增大；④方程ax2+bx+c=0有一个根大于4，其中正确的结论有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
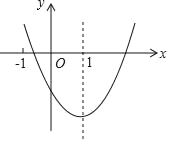
【题目】二次函数y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x＝1，下列结论①abc＞0；②b2﹣4ac＜0；③a+b+c＜0；④2a+b＝0．其中正确的是（ ）
A. ①②③ B. ②④ C. ②③ D. ①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，边长为1的正方形ABCD的对角线AC，BD相交于点O，直角∠MPN的顶点P与点O重合，直角边PM，PN分别与OA，OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是_____.
（1）EF=
OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=
；（4）OGBD=AE2+CF2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
