
【题目】用适当的方法解下列方程:
(1)x2=49 ![]()
(3)2x2+4x-3=0(公式法) (4)(x+8)(x+1)=-12
【答案】(1) x1=7,x2=-7;(2) ![]() (3)
(3) ![]() ;(4)x1=-4,x2=-5
;(4)x1=-4,x2=-5
【解析】
(1)用直接开平方法即可求解;
(2)用因式分解法即可求解;
(3)根据题意用公式法求解即可;
(4)用因式分解法即可,需注意先要将方程化为一般式.
(1)直接开平方得x=±7,
∴x1=7,x2=-7
(2)移项,得(2x+3)2-4(2x+3)=0,
分解因式,得(2x+3)[(2x+3)-4]=0,
∴2x+3=0,2x+3-4=0,
∴![]() ;
;
(3)a=2,b=4,c=-3,
b2-4ac=42-4×2×(-3)=40,
∴![]() ,
,
∴![]() ;
;
(4)化成一般式,得 x2+9x+20=0,
分解因式得 ( x+4)(x+5)=0,
∴x+4=0,x+5=0,
∴x1=-4,x2=-5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
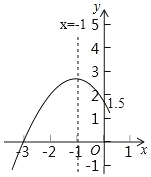
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示.
(1)确定二次函数的解析式;
(2)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
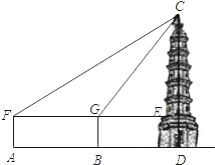
【题目】在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37° ![]() ,tan37°
,tan37° ![]() ,sin21°≈
,sin21°≈![]() ,tan21°≈
,tan21°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
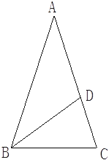
【题目】已知:如图,在△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于D,
(1)求证:△ABC∽△BCD;
(2)若BC=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
(1)求k的取值范围;
(2)若k为大于3的整数,且该方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AD=16,DE=10,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+1)x+![]() (m2+1)=0有两个相等的实数根.
(m2+1)=0有两个相等的实数根.
(1)求m的值;
(2)将y=﹣x2+(m+1)x﹣![]() (m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(m2+1)的图象向左平移3个单位长度,再向上平移2个单位长度,写出变化后函数的表达式;
(3)在(2)的条件下,当直线y=2x+n与变化后的图象有公共点时,求n2﹣4n的最小值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com