
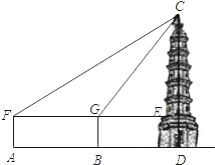
【题目】在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37° ![]() ,tan37°
,tan37° ![]() ,sin21°≈
,sin21°≈![]() ,tan21°≈
,tan21°≈![]() )
)
科目:初中数学 来源: 题型:
【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与路程的关系示意图
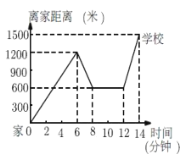
根据图中提供的信息回答下列问题
(1)小明家到学校的路程是__________米,从家到学校一共用了__________分钟.
(2)小明在书店停留了__________分钟.
(3)本次上学途中,小明12到14分行驶了__________米.12到14分的速度__________米/分.
(4)在整个上学的途中__________(哪个时间段)速度最快.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC上一个动点(不与B、C重合),在AC上取E点,使∠ADE=45度.
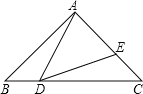
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当:△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°方向的C地有一艘渔船遇险,要求马上前去救援,要求马上前去救援.此时C地位于A地北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为12海里,则A、C两地之间的距离为________.
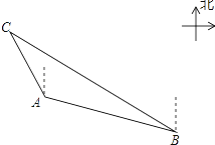
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省宁波市)在一次课题学习中,老师让同学们合作编题,某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解:
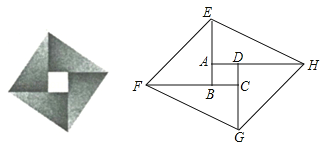
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连接EF,FG,GH,HE.
(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为美化校园,准备在长35米,宽20米的长方形场地上,修建若干条宽度相同的道路,余下部分作草坪,并请全校学生参与方案设计,现有3位同学各设计了一种方案,图纸分别如图l、图2和图3所示(阴影部分为草坪).

请你根据这一问题,在每种方案中都只列出方程不解.
①甲方案设计图纸为图l,设计草坪的总面积为600平方米.
②乙方案设计图纸为图2,设计草坪的总面积为600平方米.
③丙方案设计图纸为图3,设计草坪的总面积为540平方米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
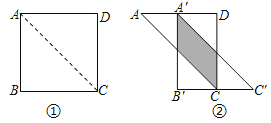
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为0.5cm2,则它移动的距离AA′等于( )
A.![]() cmB.
cmB.![]() cmC.
cmC.![]() cm或
cm或![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com