
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

【答案】(1)抛物线解析式为y=﹣![]() x2+2x+6;(2)当t=3时,△PAB的面积有最大值;(3)点P(4,6).
x2+2x+6;(2)当t=3时,△PAB的面积有最大值;(3)点P(4,6).
【解析】(1)利用待定系数法进行求解即可得;
(2)作PM⊥OB与点M,交AB于点N,作AG⊥PM,先求出直线AB解析式为y=﹣x+6,设P(t,﹣![]() t2+2t+6),则N(t,﹣t+6),由S△PAB=S△PAN+S△PBN=
t2+2t+6),则N(t,﹣t+6),由S△PAB=S△PAN+S△PBN=![]() PNAG+
PNAG+![]() PNBM=
PNBM=![]() PNOB列出关于t的函数表达式,利用二次函数的性质求解可得;
PNOB列出关于t的函数表达式,利用二次函数的性质求解可得;
(3)由PH⊥OB知DH∥AO,据此由OA=OB=6得∠BDH=∠BAO=45°,结合∠DPE=90°知若△PDE为等腰直角三角形,则∠EDP=45°,从而得出点E与点A重合,求出y=6时x的值即可得出答案.
(1)∵抛物线过点B(6,0)、C(﹣2,0),
∴设抛物线解析式为y=a(x﹣6)(x+2),
将点A(0,6)代入,得:﹣12a=6,
解得:a=﹣![]() ,
,
所以抛物线解析式为y=﹣![]()
![]() (x﹣6)(x+2)=﹣
(x﹣6)(x+2)=﹣![]() x2+2x+6;
x2+2x+6;
(2)如图1,过点P作PM⊥OB与点M,交AB于点N,作AG⊥PM于点G,
设直线AB解析式为y=kx+b,
将点A(0,6)、B(6,0)代入,得:
![]() ,
,
解得:![]() ,
,
则直线AB解析式为y=﹣x+6,
设P(t,﹣![]() t2+2t+6)其中0<t<6,
t2+2t+6)其中0<t<6,
则N(t,﹣t+6),
∴PN=PM﹣MN=﹣![]() t2+2t+6﹣(﹣t+6)=﹣
t2+2t+6﹣(﹣t+6)=﹣![]() t2+2t+6+t﹣6=﹣
t2+2t+6+t﹣6=﹣![]() t2+3t,
t2+3t,
∴S△PAB=S△PAN+S△PBN
=![]() PNAG+
PNAG+![]() PNBM
PNBM
=![]()
=![]() PNOB
PNOB
=![]() ×(﹣
×(﹣![]() t2+3t)×6
t2+3t)×6
=﹣![]() t2+9t
t2+9t
=﹣![]() (t﹣3)2+
(t﹣3)2+![]() ,
,
∴当t=3时,△PAB的面积有最大值;
(3)如图2,
∵PH⊥OB于H,
∴∠DHB=∠AOB=90°,
∴DH∥AO,
∵OA=OB=6,
∴∠BDH=∠BAO=45°,
∵PE∥x轴、PD⊥x轴,
∴∠DPE=90°,
若△PDE为等腰直角三角形,
则∠EDP=45°,
∴∠EDP与∠BDH互为对顶角,即点E与点A重合,
则当y=6时,﹣![]() x2+2x+6=6,
x2+2x+6=6,
解得:x=0(舍)或x=4,
即点P(4,6).


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,DE垂直平分斜边AB,分别交AB、BC于D、E.若∠CAB=∠B+30°,CE=2cm.
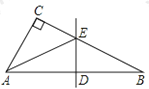
求:(1)∠AEB 度数.
(2)BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生对篮球、足球、排球、羽毛球、乒乓球这五种球类运动的喜爱情况,随机抽取一部分学生进行问卷调查,统计整理并绘制了以下两幅不完整的统计图:

请根据以上统计图提供的信息,解答下列问题:
(1)共抽取 名学生进行问卷调查;
(2)补全条形统计图,求出扇形统计图中“足球”所对应的圆心角的度数;
(3)该校共有3000名学生,请估计全校学生喜欢足球运动的人数.
(4)甲乙两名学生各选一项球类运动,请求出甲乙两人选同一项球类运动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?
(1)设江水的流速为![]() 千米/时,填空:轮船顺流航行速度为_________千米/时,逆流航行速度为_________千米/时,顺流航行100千米所用时间为_________小时,逆流航行60千米所用时间为_________小时.
千米/时,填空:轮船顺流航行速度为_________千米/时,逆流航行速度为_________千米/时,顺流航行100千米所用时间为_________小时,逆流航行60千米所用时间为_________小时.
(2)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】维修一项工程,甲、乙两队合做,![]() 天能完成,共付工钱
天能完成,共付工钱![]() 元,甲队每天的工钱比乙队多
元,甲队每天的工钱比乙队多![]() 元.若两队独做,乙队工期是甲队的
元.若两队独做,乙队工期是甲队的![]() 倍.
倍.
(1)甲、乙两队独做各需多少天完成?
(2)若两队独做,哪队工钱总额较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.
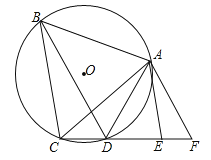
(1)求证:EA是⊙O的切线;
(2)求证:BD=CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以直角三角形的各边边边分别向外作正三角形,再把较小的两张正三角形纸片按图2的方式放置在最大正三角形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积B.较小两个正三角形重叠部分的面积
C.最大正三角形的面积D.最大正三角形与直角三角形的面积差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展我市旅游经济,丹东天桥沟景区对门票采用动态的售票方法吸引游客,规定:门票定价为100元/人,非节假日打![]() 折售票,节假日按团队人数分段定价售票,即10人以下(含10人)的团队按原价售票;超过10人的团队,其中10人仍按原价售票,超过10人部分的游客打
折售票,节假日按团队人数分段定价售票,即10人以下(含10人)的团队按原价售票;超过10人的团队,其中10人仍按原价售票,超过10人部分的游客打![]() 折售票。设某旅游团人数为
折售票。设某旅游团人数为![]() 人,非节假日购票款为
人,非节假日购票款为![]() (元),节假日购票款为
(元),节假日购票款为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)观察图象可知:![]() _______,
_______,![]() __________;
__________;
(2)直接写出![]() 和
和![]() 的函数关系式(不需要写出自变量的取值范围);
的函数关系式(不需要写出自变量的取值范围);
(3)导游小王10月1日带![]() 团,10月20日(非节假日)带
团,10月20日(非节假日)带![]() 团都到天桥沟景区旅游,共付门票款4600元,
团都到天桥沟景区旅游,共付门票款4600元,![]() 、
、![]() 两个团队合计60人,求
两个团队合计60人,求![]() 、
、![]() 两个团队各有多少人?
两个团队各有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
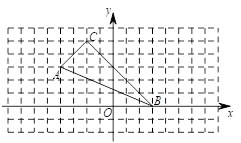
【题目】在平面直角坐标系xOy中,△ABC的位置如图所示.
(1)分别写出以下顶点的坐标:A( , );B( , ) ;C( , ).
(2)顶点A关于x轴对称的点A′的坐标( , ),顶点C关于y轴对称的点C′的坐标( , ).
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com