
【题目】如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.
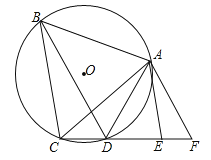
(1)求证:EA是⊙O的切线;
(2)求证:BD=CF.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据等边三角形的性质可得:∠OAC=30°,∠BCA=60°,证明∠OAE=90°,可得:AE是⊙O的切线;
(2)先根据等边三角形性质得:AB=AC,∠BAC=∠ABC=60°,由四点共圆的性质得:∠ADF=∠ABC=60°,得△ADF是等边三角形,证明△BAD≌△CAF,可得结论.
(1)连接OA.
∵⊙O是等边三角形ABC的外接圆,∴∠OAC=30°,∠BCA=60°.
∵AE∥BC,∴∠EAC=∠BCA=60°,∴∠OAE=∠OAC+∠EAC=30°+60°=90°,∴AE是⊙O的切线;
(2)∵△ABC是等边三角形,∴AB=AC,∠BAC=∠ABC=60°.
∵A、B、C、D四点共圆,∴∠ADF=∠ABC=60°.
∵AD=DF,∴△ADF是等边三角形,∴AD=AF,∠DAF=60°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF.
在△BAD和△CAF中,∵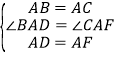 ,∴△BAD≌△CAF,∴BD=CF.
,∴△BAD≌△CAF,∴BD=CF.


科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学试验(用纸签D、E、F表示)中各抽取一个实验操作进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.用列表或画树状图的方法求小刚抽到物理实验B和化学实验F的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A,B,把抛物线与线段AB围成的图形记为C1, 将Cl绕点B中心对称变换得C2, C2与x轴交于另一点C,将C2绕点C中心对称变换得C3, 连接C与C3的顶点,则图中阴影部分的面积为( )
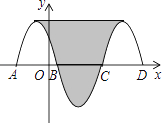
A. 32 B. 24 C. 36 D. 48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,得
,得![]() ;
;![]() 与
与![]() 的平分线相交于点
的平分线相交于点![]() ,得
,得![]() ;……;
;……;![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,要使
,要使![]() 的度数为整数,则
的度数为整数,则![]() 的最大值为( )
的最大值为( )
A.4B.5C.6D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的部分图象如图所示,与x轴的一个交点坐标为
的部分图象如图所示,与x轴的一个交点坐标为![]() ,抛物线的对称轴是
,抛物线的对称轴是![]() 下列结论中:
下列结论中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有两个不相等的实数根;
有两个不相等的实数根;![]() 抛物线与x轴的另一个交点坐标为
抛物线与x轴的另一个交点坐标为![]() ;
;![]() 若点
若点![]() 在该抛物线上,则
在该抛物线上,则![]() .
.
其中正确的有![]()
![]()
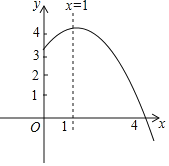
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=30°,点B在射线AM上,且 AB=6,点C在射线AN上.

(1)若△ABC是直角三角形,求AC的长;
(2)若△ABC是等腰三角形,则满足条件的C点有 个;
(3)设BC=x,当△ABC唯一确定时, 直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com