
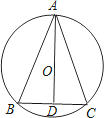
【题目】如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
【答案】证明见解析.
【解析】
试题(1)过点D作DE⊥AB于点E,DF⊥AC于点F,根据HL定理可得出△BDE≌△CDF,进而得出结论;
(2)根据等腰三角形三线合一的性质可知AD⊥BC,再由BD=CD,可知AD过圆心O,故可得出结论.
试题解析:(1)答:△ABC是等腰三角形.
证明:过点D作DE⊥AB于点E,DF⊥AC于点F.

∵AD是角平分线,
∴DE=DF.
又∵AD是△ABC的中线,
∴BD=CD,
在Rt△BDE与Rt△CDF中,
![]() ,
,
∴△BDE≌△CDF(HL).
∴∠B=∠C,
∴AB=AC,即△ABC是等腰三角形;
(2)答:AD过△ABC的外接圆圆心O,⊙O是△ABC的外接圆.
证明:∵AB=AC,AD是角平分线,
∴AD⊥BC,
又∵BD=CD,
∴AD过圆心O.
作边AB的中垂线交AD于点O,交AB于点M,则点O就是△ABC的外接圆圆心,
∴⊙O是△ABC的外接圆.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】小明解方程![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以(x-2),得1-(1-x)=3(第一步)
去括号,得1-1+x=3(第二步)
移项,合并同类项,得x=3(第三步)
检验,当x=3时x-2≠0(第四步)
所以x=3是原方程的解.(第五步)
(1)小明解答过程是从第____步开始出错的,原方程化为第一步的根据是_____.
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 在反比例函数图象上,
在反比例函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
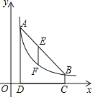
(1)求![]() ,
,![]() 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
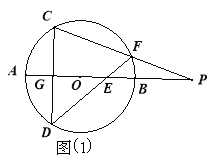
(1)如图1,当点E在直径AB上时,试证明:![]()
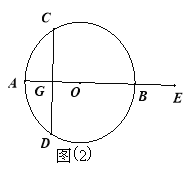
(2)当点E在直径AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
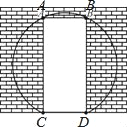
【题目】如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=![]() 米.
米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
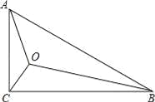
【题目】如图,在Rt△ABC中,∠C=90°,AC=1,BC=![]() ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=______,OA+OB+OC=______.
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=______,OA+OB+OC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABPD的边长为3,将边DP绕点P顺时针旋转90°至PC,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF,连接BE并延长分别交DF、DC于H、G.
(1)①求证:△BPE≌△DPF,②判断BG与DF位置关系并说明理由;
(2)当PE的长度为多少时,四边形DEFG为菱形并说明理由;
(3)连接AH,在点E、F运动的过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请求出∠AHB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
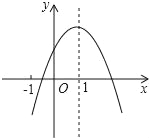
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com