
【题目】已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
(1)如图1,当点E在直径AB上时,试证明:![]()
(2)当点E在直径AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】
试题(1)如图,连接FO并延长交⊙O于Q,连接DQ.由FQ是⊙O直径得到∠QFD+∠Q=90°,又由CD⊥AB得到∠P+∠C=90°,然后利用已知条件即可得到∠QFD=∠P,然后即可证明△FOE∽△POF,最后利用相似三角形的性质即可解决问题;
(2)(1)中的结论成立.如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.由FM是⊙O直径得到∠M+∠CFM=90°,又由CD⊥AB,得到∠E+∠D=90°,接着利用已知条件即可证明∠CFM=∠E,然后利用已知条件证明△POF∽△FOE,最后利用相似三角形的性质即可证明题目的结论.
试题解析:(1)证明:如图1,连接FO并延长交⊙O于Q,连接DQ.
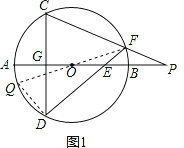
∵FQ是⊙O直径,
∴∠FDQ=90°.
∴∠QFD+∠Q=90°.
∵CD⊥AB,
∴∠P+∠C=90°.
∵∠Q=∠C,
∴∠QFD=∠P.
∵∠FOE=∠POF,
∴△FOE∽△POF.
∴![]() .
.
∴OEOP=OF2=r2.
(2)解:(1)中的结论成立.
理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
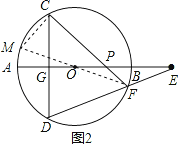
∵FM是⊙O直径,
∴∠FCM=90°,
∴∠M+∠CFM=90°.
∵CD⊥AB,
∴∠E+∠D=90°.
∵∠M=∠D,
∴∠CFM=∠E.
∵∠POF=∠FOE,
∴△POF∽△FOE.
∴![]() ,
,
∴OEOP=OF2=r2.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
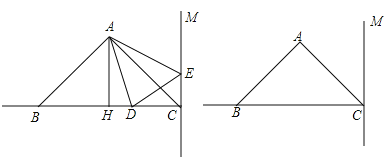
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
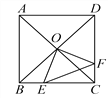
【题目】如图,正方形ABCD中,AB=8cm,对角线AC、BD相交于点O,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CD运动,到点C、D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
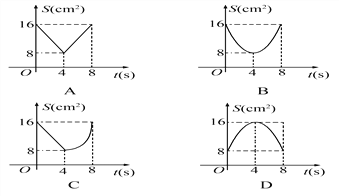
A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
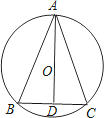
【题目】如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
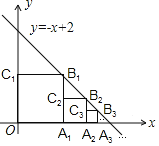
【题目】正方形![]() 、
、![]() 、
、![]() …按如图放置,其中点
…按如图放置,其中点![]() 、
、![]() 、
、![]() …在
…在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,依此类推…,则点
上,依此类推…,则点![]() 的坐标是________;点
的坐标是________;点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com