
【题目】解方程
(1)![]()
(2)![]()
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)观察可得二次项系数为1,故把常数项移项到右边,两边都加上一次项系数一半的平方,即加上4,左边化为完全平方式,右边是非负常数,开方转化为两个一元一次方程,求出两方程的解即可得到原方程的解;
(2)利用十字相乘法把方程左边的多项式分解因式,然后根据两数积为0,两数至少有一个为0化为两个一元一次方程,求出两方程的解即可得到原方程的解.
解:(1)x2-4x-2=0,
移项得:x2-4x=2,
两边都加上4得:(x-2)2=6,
开方得:x-2=![]() 或x-2=-
或x-2=-![]() ,
,
∴x1=2+![]() ,x2=2-
,x2=2-![]() ;
;
(2)3x2-2x-5=0,
因式分解得:(3x-5)(x+1)=0,
可化为:3x-5=0或x+1=0,
∴x1=![]() ,x2=-1.
,x2=-1.


科目:初中数学 来源: 题型:
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低,若该果园每棵果树产果y千克,增种果树x棵,它们之间的函数关系如图所示.

(1)求y与x之间的函数解析式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过D作DE⊥AC于E,AB-BC=4,AC=8,则△ABP面积为_____
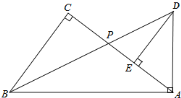
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 在反比例函数图象上,
在反比例函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
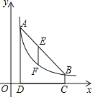
(1)求![]() ,
,![]() 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
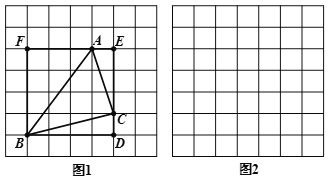
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
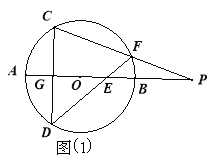
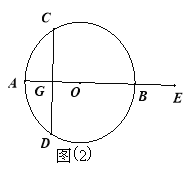
(1)如图1,当点E在直径AB上时,试证明:![]()
(2)当点E在直径AB(或BA)的延长线上时,以如图2点E的位置为例,请你画出符合题意的图形,标注上字母,(1)中的结论是否成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
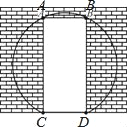
【题目】如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=![]() 米.
米.
(1)求此圆形门洞的半径;
(2)求要打掉墙体的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABPD的边长为3,将边DP绕点P顺时针旋转90°至PC,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF,连接BE并延长分别交DF、DC于H、G.
(1)①求证:△BPE≌△DPF,②判断BG与DF位置关系并说明理由;
(2)当PE的长度为多少时,四边形DEFG为菱形并说明理由;
(3)连接AH,在点E、F运动的过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请求出∠AHB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆(平行于AB)的矩形花圃.设花圃的一边AB为xm,面积为ym2.
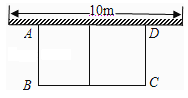
(1)求y与x的函数关系式;
(2)如果要围成面积为63m2的花圃,AB的长是多少?
(3)能围成比63m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com