
【题目】已知,正方形ABPD的边长为3,将边DP绕点P顺时针旋转90°至PC,E、F分别为线段DP、CP上两个动点(不与D、P、C重合),且DE=CF,连接BE并延长分别交DF、DC于H、G.
(1)①求证:△BPE≌△DPF,②判断BG与DF位置关系并说明理由;
(2)当PE的长度为多少时,四边形DEFG为菱形并说明理由;
(3)连接AH,在点E、F运动的过程中,∠AHB的大小是否发生改变?若改变,请说出是如何变化的;若不改变,请求出∠AHB的度数.

【答案】(1)①见解析,②BG⊥DF;(2)当PE=3![]() ﹣3时,四边形DEFG为菱形;
﹣3时,四边形DEFG为菱形;
(3)45°.
【解析】分析:
(1)①由已知条件易得BP=DP=PC,∠BPE=∠DPF=90°结合DE=CF可得PE=PF,由此即可得到△BPE≌△DPF;②由△BPE≌△DPF可得∠EBP=∠FDP,结合∠FDP+∠BFH=90°,可得∠EBP+∠BFH=90°,从而可得∠BHP=90°,由此可得BG⊥DF;
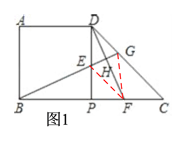
(2)如下图1,连接EF、GF,由题意可知,要使四边形DEFG是菱形,则必须使DE=EF,由(1)中所得△BPE≌△DPF可得PF=PE,设PE=x,则DE=3-x=EF,由此在Rt△PEF中由勾股定理建立方程,解方程即可求得此时PE=x=![]() ,解题时把PE=
,解题时把PE=![]() 作为一个条件,结合题目中的其它条件去证明此时四边形DEFG为菱形即可;
作为一个条件,结合题目中的其它条件去证明此时四边形DEFG为菱形即可;
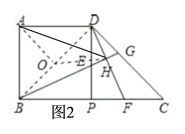
(3)如图2,连接BD,作出BD的中点O,连接AO,HO,由已知条件结合(1)中所得BG⊥DF易得OA=OB=OD=OH=![]() BD,由此可得点A、B、H、D在以O为圆心、OA为半径的圆上,从而可得∠AHB=∠ADB=45°.
BD,由此可得点A、B、H、D在以O为圆心、OA为半径的圆上,从而可得∠AHB=∠ADB=45°.
详解:
(1)①证明:由旋转的性质可知,△DPC是等腰直角三角形,
∵四边形ABPD是正方形,
∴BP=PD=PC,∠BPE=∠DPF=90°,
∵DE=CF,
∴PE=PF,
在△BPE和△DPF中,
BP=PD,∠BPE=∠DPF,PE=PF,
∴△BPE≌△DPF;
②∵△BPE≌△DPF,
∴∠EBP=∠FDP,又∠FDP+∠BFH=90°,
∴∠EBP+∠BFH=90°,
∴∠BHP=90°,
∴BG⊥DF;
(2)当PE=![]() 时,四边形DEFG为菱形;理由如下:
时,四边形DEFG为菱形;理由如下:
在正方形ABPD中,BP=PD=3,
∵PE=![]() ,EF=PE,
,EF=PE,
∴EF=![]() =6﹣3
=6﹣3![]() ,DE=PD-PE=6﹣3
,DE=PD-PE=6﹣3![]() ,
,
∴EF=ED,
∵BG⊥DF,
∴EG垂直平分DF,
∴GD=GF,
∵∠PEF=∠PDC=45°,
∴EF∥DG,
∴∠EFD=∠FDG,
∵DE=EF,
∴∠EFD=∠EDF,
∴∠EDG=∠FDE,
∵BG⊥DF,
∴∠DEG=∠DGE,
∴DE=DG,
∴DE=DG=GF=EF,
∴四边形DEFG是菱形;
(3)∠AHB的大小不变,∠AHB=45°,
连接BD,取BD的中点O,连接OA、OH,
∵四边形ABCD是正方形,
∴∠BAD=90°,∠ADB=45°,
∵BG⊥DF,
∴∠DHB=90°,
则OA=OB=OD=OH=![]() BD,
BD,
∴点A、B、H、D在以O为圆心、OA为半径的圆上,
∴∠AHB=∠ADB=45°.


科目:初中数学 来源: 题型:
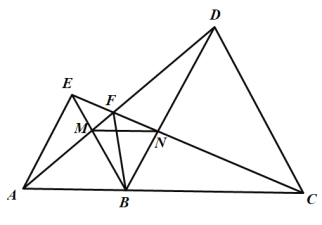
【题目】如图,![]() ,
,![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,下列结论正确的有_________.
,下列结论正确的有_________.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
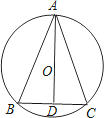
【题目】如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
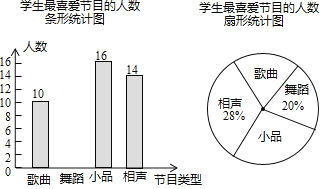
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 、
、![]() 、
、![]() …按如图放置,其中点
…按如图放置,其中点![]() 、
、![]() 、
、![]() …在
…在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,依此类推…,则点
上,依此类推…,则点![]() 的坐标是________;点
的坐标是________;点![]() 的坐标是_________.
的坐标是_________.
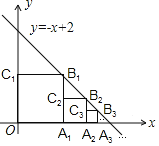
查看答案和解析>>
科目:初中数学 来源: 题型:
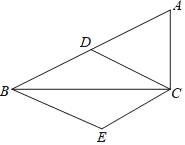
【题目】如图,点D是Rt△ABC斜边AB的中点,过点B、C分别作BE∥CD,CE∥BD.
(1)若∠A=60°,AC=![]() ,求CD的长;
,求CD的长;
(2)求证:BC⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
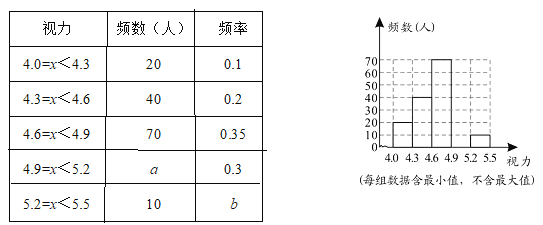
【题目】某校为了解八年级学生的视力情况,对八年级学生进行了一次视力调查,并将调查结果进行统计整理,绘制了频数分布表和频数分布直方图的一部分.
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若将视力在4.6及以上的视力情况定义为“视力正常”,求“视力正常”的人数占被调查人数的百分比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com