
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
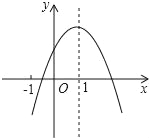
【答案】①③④⑥
【解析】
①由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴位置确定b的符号,可对①作判断;
②根据a和c的符号可得:a-c<0,根据b的符号可作判断;
③根据对称性可得:当x=2时,y>0,可作判断;
④根据对称轴为:x=1可得:a=-![]() b,结合x=-1时,y<0,可作判断;
b,结合x=-1时,y<0,可作判断;
⑤根据顶点坐标的纵坐标为最大值可作判断;
⑥根据2a+b=0和c>0可作判断.
解:①∵该抛物线开口方向向下,∴a<0.
∵抛物线对称轴在y轴右侧,∴a、b异号,∴b>0;
∵抛物线与y轴交于正半轴,∴c>0,
∴abc<0;
故①正确;
②∵a<0,c>0,∴ac<0,
∵b>0,∴b>ac,
故②错误;
③根据抛物线的对称性知,当x=2时,y>0,即4a+2b+c>0;故③正确;
④∵对称轴方程x=![]() =1,∴b=2a,∴a=
=1,∴b=2a,∴a=![]() b,
b,
∵当x=1时,y=ab+c<0,∴![]() b+c<0,
b+c<0,
∴2c<3b,
故④正确;
⑤∵x=m对应的函数值为y=am2+bm+c,
x=1对应的函数值为y=a+b+c,
又x=1时函数取得最大值,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm=m(am+b),
故⑤错误;
⑥∵b=2a,∴2a+b=0,
∵c>0,
∴2a+b+c>0,
故⑥正确.
综上所述,其中正确的结论的有:①③④⑥.
故答案为:①③④⑥.


科目:初中数学 来源: 题型:
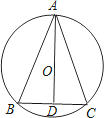
【题目】如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
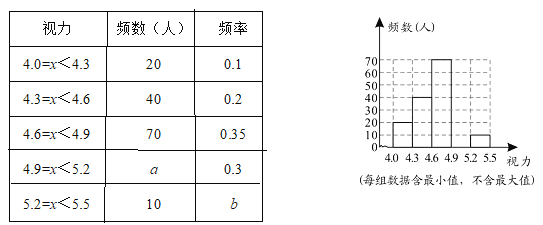
【题目】某校为了解八年级学生的视力情况,对八年级学生进行了一次视力调查,并将调查结果进行统计整理,绘制了频数分布表和频数分布直方图的一部分.
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若将视力在4.6及以上的视力情况定义为“视力正常”,求“视力正常”的人数占被调查人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
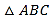
查看答案和解析>>
科目:初中数学 来源: 题型:
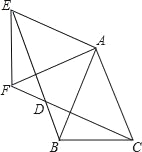
【题目】如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
(1)求证:BE=CF;
(2)当四边形ACDE为平行四边形时,求证:△ABE为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里有5个小球,分别标有数字﹣3,﹣2,﹣1,﹣![]() ,﹣
,﹣![]() ,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
(1)用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率.
(2)若以第一次摸出球上的数字为横坐标,第二次摸出球上的数字为纵坐标确定一点,直接写出该点在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
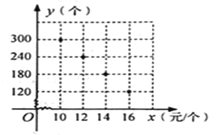
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大的利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com