
����Ŀ��ijУ������Ա�μ���ṫ����������һ����Ըƿ�������ۣ������������������ƻ���.�����г����飬������Ըƿһ��ʱ���ڵ�������y�����������۵���x��Ԫ/����֮��Ķ�Ӧ��ϵ��ͼ��ʾ��
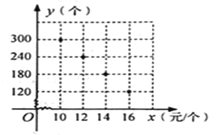
��1�����ж�y��x֮��ĺ�����ϵ�������������ϵʽ��
��2������Ըƿ�Ľ���Ϊ6Ԫ/�������������г���������۹��ɣ�����������w��Ԫ�������۵���x��Ԫ/����֮��ĺ�����ϵʽ��
��3���ڣ�2���������£�����Ըƿ�Ľ����ɱ�������900Ԫ��Ҫ��������������ȷ��������Ըƿ�����۵��ۣ��������ʱ���������.
���𰸡���1��y=-30x+600����2��![]() ����3��x=15ʱ���������1350Ԫ.
����3��x=15ʱ���������1350Ԫ.
��������
���⣨1���۲�ɵøú���ͼ����һ�κ��������һ�κ�������ʽ��������������뼴����øú�������ʽ����������������ĺ�������뿴�������Ƿ�������������ͬ��
��2����������=ÿ����Ըƿ����������������
��3�����ݽ����ɱ��ɵ��Ա�����ȡֵ����϶��κ����Ĺ�ϵʽ���������Ӧ���������
�����������1��y��x��һ�κ�������y=kx+b��
ͼ����㣨10��300������12��240����
![]() ��
��
���![]() ��
��
��y=-30x+600��
��x=14ʱ��y=180����x=16ʱ��y=120��
���㣨14��180������16��120�����ں���y=-30x+600ͼ���ϣ�
��y��x֮��ĺ�����ϵʽΪy=-30x+600��
��2��w=��x-6����-30x+600��=-30x2+780x-3600��
��w��x֮��ĺ�����ϵʽΪw=-30x2+780x-3600��
��3��������ã�6��-30x+600����900��
���x��15��
w=-30x2+780x-3600ͼ��Գ���Ϊ��x=-![]() =-
=-![]() =13��
=13��
��a=-30��0��
�������߿������£���x��15ʱ��w��x�������С��
����x=15ʱ��w���=1350��
����15Ԫ/���ļ۸�����������Ըƿ�ɻ���������1350Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
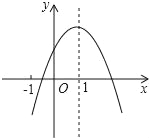
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��������6�����ۣ�
��abc��0��
��b��a��c��
��4a+2b+c��0��
��2c��3b��
��a+b��m��am+b������m��1��ʵ����
��2a+b+c��0��������ȷ�Ľ��۵���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=a��x��1����x��3����a��0����x�ύ��A��B���㣬������������һ��C��x���·�����ʹ��OCA�ס�OBC��
��1�����߶�OC�ij��ȣ�
��2����ֱ��BC��y�ύ�ڵ�M����C��BM���е�ʱ����ֱ��BM�������ߵĽ���ʽ��
��3���ڣ�2���������£�ֱ��BC�·����������Ƿ����һ��P��ʹ���ı���ABPC�����������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����Ϊ�˽�ijС������ʹ�ù��������������ij�о�С������ɷø�С����10λ���õ���10λ����һ����ʹ�ù��������Ĵ����ֱ�Ϊ��17��12��15��20��17��0��7��26��17��9��
��1���������ݵ���λ������ ������������ ����
��2��������10λ����һ����ʹ�ù���������ƽ��������
��3������С����200�������Թ��Ƹ�С������һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ��һֱ��l1:y=-x+3�ֱ���x�ᡢy�ύ��A��B���㣬������y=-x2+bx+c����A��B���㣬y���Ҳಿ������������һ����C������C��y���ƽ���߽�ֱ��l1�ڵ�D.
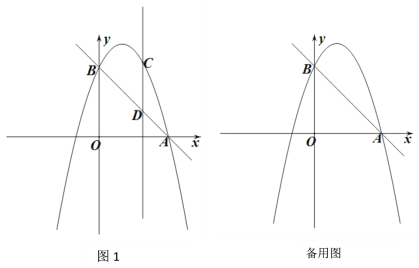
��1���������ߵĺ�������ʽ��
��2����ͼ1��C�ڵ�һ���ޣ�����CDΪֱ������E�������������жϴ�ʱ��E�������ߵĶԳ����Ƿ��������������У����ʹ����E��������߶Գ�������ʱ��C�ĺ����ꣻ
��3������ƽ�����Ƿ���ڵ�M��ʹB��C��D��MΪ������ı���Ϊ�����������ڣ�ֱ��д����M�����ꣻ�����ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
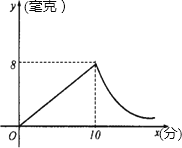
����Ŀ��ΪԤ��������ڲ�����ijУ�Խ��ҽ��С�ҩѬ����������֪ҩ��ȼ�սΣ�����ÿ���������еĺ�ҩ��y�����ˣ���ȼ��ʱ��x�����ӣ�����������ȼ�սκ�y��x�ɷ�����������������֮��Ĺ�ϵ��ͼ��ʾ�����ֲ��ҩ��10����ȼ�꣬��ʱ������ÿ����������ҩ��Ϊ8���ˣ���������Ϣ����������⣺
��1����ҩ��ȼ��ʱy��x�ĺ�������ʽ��
��2����ҩ��ȼ�սκ�y��x�ĺ�������ʽ��
��3������ҩѬ������ʱ�䵽50����ʱ��ÿ���������еĺ�ҩ�������巽���������ã���ô����ҩѬ������ʱ�䵽50����ʱÿ���������еĺ�ҩ��Ϊ���ٺ��ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��![]() ��
��![]() ����
����![]() ��������ת�任�����εõ�
��������ת�任�����εõ�![]() ����
����![]() ��ֱ�Ƕ��������Ϊ__________��
��ֱ�Ƕ��������Ϊ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������10�֣���ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��
��![]() ��������
Ϊ��������![]() ����ͼ����A��1��a����B���㣮
����ͼ����A��1��a����B���㣮
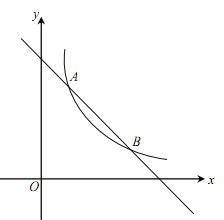
��1�����������ı���ʽ����B�����ꣻ
��2����x������һ��P��ʹPA+PB��ֵ��С�������������ĵ�P�����꼰��PAB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У���E�ڱ�CD�ϣ���P���߶�AE�ϣ��ҵ�A��B��D��������ľ���ֱ�Ϊ![]() ��2
��2![]() ��6�����ı���BCDP�����Ϊ_____��
��6�����ı���BCDP�����Ϊ_____��
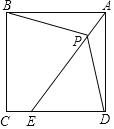
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com