
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
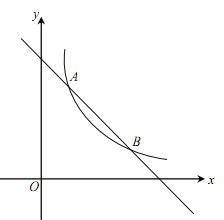
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
【答案】(1)![]() ,
,![]() ;(2)P
;(2)P![]() ,
,![]() .
.
【解析】
试题(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=![]() ,
,
得:3=k,
∴反比例函数的表达式y=![]() ,
,
联立两个函数关系式成方程组得: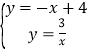 ,
,
解得:![]() ,或
,或![]() ,
,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.

∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得:![]() ,
,
解得:![]() ,
,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(3-1)-
×[1-(-1)]×(3-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里有5个小球,分别标有数字﹣3,﹣2,﹣1,﹣![]() ,﹣
,﹣![]() ,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
(1)用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率.
(2)若以第一次摸出球上的数字为横坐标,第二次摸出球上的数字为纵坐标确定一点,直接写出该点在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
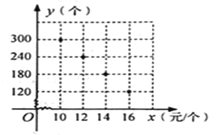
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大的利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法.
问题提出:求边长分别为、![]() 、
、![]() 、
、![]() 的三角形面积.
的三角形面积.
问题解决:
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
![]() 、
、![]() 、
、![]() 的格点三角形
的格点三角形![]() (如图),
(如图),![]() 是角边为1和2的直角三角形斜边,
是角边为1和2的直角三角形斜边,![]() 是直角边分别为1和3的直角三角形的斜边,
是直角边分别为1和3的直角三角形的斜边,![]() 是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求
是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求![]() 的高,而借用网格就能计算它的面积.
的高,而借用网格就能计算它的面积.
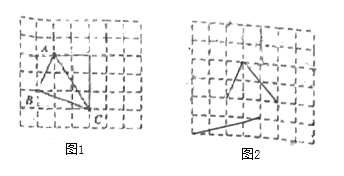
(1)请直接写出图①中![]() 的面积为____________.
的面积为____________.
(2)类比迁移:求边长分别为![]() 、
、![]() 、
、![]() 的三角形面积(请利用图②的正方形网格画出相应的
的三角形面积(请利用图②的正方形网格画出相应的![]() ,并求出它的面积)
,并求出它的面积)
(3)思维拓展:求边长分别为![]() ,的三角形的面积
,的三角形的面积
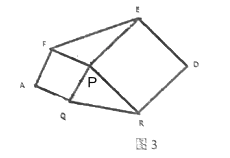
(4)如图(3),已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,正方形
,正方形![]() ,连接
,连接![]() ,若
,若![]() ,则六边形
,则六边形 ![]() 的面积是_________.
的面积是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
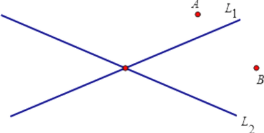
【题目】如图,A、B是两个工厂,L1、L2是两条公路,现要在这一地区建一加油站,要求加油站到A、B两厂的路程相等,且到两条路的距离相等,请用尺规作图找出符合条件的点P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
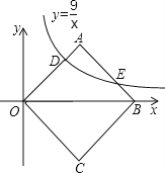
【题目】如图,Rt△AOB中,∠OAB=90°,OA=AB,将Rt△AOB放置于直角坐标系中,OB在x轴上,点O是原点,点A在第一象限.点A与点C关于x轴对称,连结BC,OC.双曲线![]() (x>0)与OA边交于点D、与AB边交于点E.
(x>0)与OA边交于点D、与AB边交于点E.
(1)求点D的坐标;
(2)求证:四边形ABCD是正方形;
(3)连结AC交OB于点H,过点E作EG⊥AC于点G,交OA边于点F,求四边形OHGF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:等腰三角形两腰上的高相等.

(1)请你写出它的逆命题:______.
(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com