
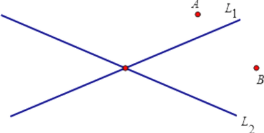
【题目】如图,A、B是两个工厂,L1、L2是两条公路,现要在这一地区建一加油站,要求加油站到A、B两厂的路程相等,且到两条路的距离相等,请用尺规作图找出符合条件的点P.
【答案】见解析
【解析】
连接AB,作线段AB的垂直平分线,再作∠COD的角平分线,线段AB的垂直平分线和∠COD的角平分线的交点即为P点,作∠COD的外角平分线,∠COD的外角平分线和线段AB的垂直平分线的交点为P′.
解:如图所示
第一步:作AB的垂直平分线:连接AB,以A为圆心,大于![]() AB的长度为半径画弧,以B为圆心,大于
AB的长度为半径画弧,以B为圆心,大于![]() AB的长度为半径画弧,过两弧的交点作AB的垂线;
AB的长度为半径画弧,过两弧的交点作AB的垂线;
第二步:作∠COD的角平分线:以O为圆心,任意长度为半径画弧,分别与射线OC和射线OD交于E、F,再以E为圆心,大于![]() EF的长度为半径画弧,以F为圆心,大于
EF的长度为半径画弧,以F为圆心,大于![]() EF的长度为半径画弧,连接OM,射线OM与AB的垂直平分线的交点就是P点;
EF的长度为半径画弧,连接OM,射线OM与AB的垂直平分线的交点就是P点;
同理可得:作∠COD的外角平分线,∠COD的外角平分线与AB的垂直平分线的交点为P′.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
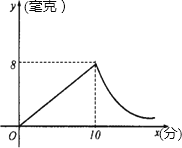
【题目】为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(毫克)与燃烧时间x(分钟)成正比例;燃烧阶段后,y与x成反比例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题:
(1)求药物燃烧时y与x的函数解析式.
(2)求药物燃烧阶段后y与x的函数解析式.
(3)当“药熏消毒”时间到50分钟时,每立方米空气中的含药量对人体方能无毒害作用,那么当“药熏消毒”时间到50分钟时每立方米空气中的含药量为多少毫克?
查看答案和解析>>
科目:初中数学 来源: 题型:
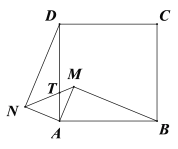
【题目】如图,在Rt△ABM和Rt△ADN的斜边分别为正方形的边AB和AD,其中AM=AN.
(1)求证:Rt△ABM≌Rt△AND
(2)线段MN与线段AD相交于T,若AT=![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
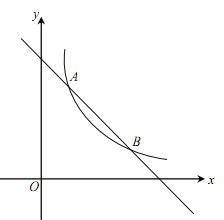
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC⊥y轴,BC<OA,点A,点C分别在x轴、y轴的正半轴上,D是线段BC上一点,BD=![]() OA=
OA=![]() ,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两动点,且始终保持∠DEF=45°.将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为______.
,AB=3,∠OAB=45°,E,F分别是线段OA,AB上的两动点,且始终保持∠DEF=45°.将△AEF沿一条边翻折,翻折前后两个三角形组成的四边形为菱形,则线段OE的值为______.
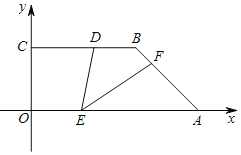
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点O为AB中点,点P为直线BC上的动点(不与点B、点C重合),连接OC、OP,将线段OP绕点P顺时针旋转60°,得到线段PQ,连接BQ.
(1)如图1,当点P在线段BC上时,请直接写出线段BQ与CP的数量关系.
(2)如图2,当点P在CB延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)如图3,当点P在BC延长线上时,若∠BPO=15°,BP=4,请求出BQ的长.
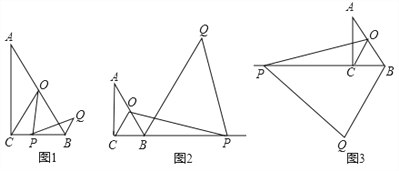
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:阿基米德折弦定理:如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.下面是运用“截长法”证明CD=AB+BD的部分证明过程.
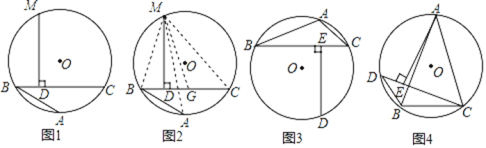
证明:如图2,在CB上截取CG=AB,连接MA,MB,MC和MG
∵M是![]() 的中点,
的中点,
∴MA=MC
……
请按照上面的证明思路,写出该证明的剩余部分;
实践应用:
(1)如图3,已知△ABC内接于⊙O,BC>AB>AC,D是![]() 的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为BE=CE+ACBE=CE+AC;
的中点,依据阿基米德折弦定理可得图中某三条线段的等量关系为BE=CE+ACBE=CE+AC;
(2)如图4,已知等腰△ABC内接于⊙O,AB=AC,D为![]() 上一点,连接DB,∠ACD=45°,AE⊥CD于点E,△BCD的周长为4
上一点,连接DB,∠ACD=45°,AE⊥CD于点E,△BCD的周长为4![]() +2,BC=2,请求出AC的长.
+2,BC=2,请求出AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E是CD的中点,连接BE并延长交AD延长线于点F.
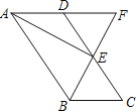
(1)求证:点D是AF的中点;
(2)若AB=2BC,连接AE,试判断AE与BF的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com