【题目】如图，在△ABC 中，AB=AC，∠C=70°，△AB′C′与△ABC 关于直线 EF对称，∠CAF=10°，连接 BB′，则∠ABB′的度数是（ ）
A. 30° B. 35° C. 40° D. 45°
科目：初中数学 来源： 题型：
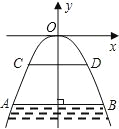
【题目】如图所示，有一座抛物线形拱桥，桥下面在正常水位时，AB宽20 m，水位上升到警戒线CD时，CD到拱桥顶E的距离仅为1 m，这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式；
(2)若洪水到来时，水位以每小时0.3 m的速度上升，从正常水位开始，持续多少小时到达警戒线？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据题意，解答问题：
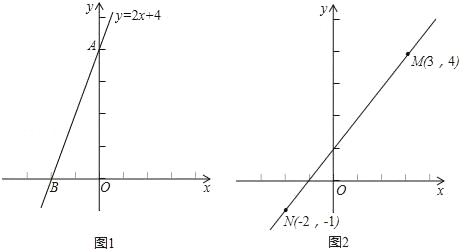
（1）如图1，已知直线y=2x+4与x轴、y轴分别交于A、B两点，求线段AB的长.
（2）如图2，类比（1）的解题过程，请你通过构造直角三角形的方法，求出点M（3，4）与点N（﹣2，﹣1）之间的距离.
（3）在（2）的基础上，若有一点D在x轴上运动，当满足DM=DN时，请求出此时点D的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC在平面直角坐标系中的位置如图所示，先将△ABC向右平移3个单位，再向下平移1个单位到△A1B1C1，△A1B1C1和△A2B2C2关于x轴对称
(1)画出△A1B1C1和△A2B2C2
(2)在x轴上确定一点P，使BP＋A1P的值最小，直接写出P的坐标为________
(3)点Q在坐标轴上且满足△ACQ为等腰三角形，则这样的Q点有 个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B=100° ，按要求完成画图并解答问题：
（1）画出△ABC的高CE，中线AF，角平分线BD，且AF所在直线交CE于点H，BD与AF相交于点G；
（2）若∠FAB=40°，求∠AFB的度数和∠BCE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图1，直线l1∥x轴，直线l2为第一、三象限的角平分线，直线l1与l2相交于A（3，3），点B为直越l1上一点，点C为x轴上一点，P（x，y）为一动点．
（1）当点P（x，y）在x轴上时，y= ，当点P（x，y）在直线l1上，y= ，当点P（x，y）在直线l2上时y= ．
如图1，当点P在直线l1下方、x轴上方、直线l2左上方区域时，x，y满足如下条件：
，则∠APO，∠PAB，∠POC的数量关系是 ．
如图2，当点P在直线l1下方、x轴上方、直线l2右下方区域时，x，y满足如下条件：
，则∠APO，∠PAB，∠POC的数量关系是 ．
（2）当点P在直线l1上方区域，且点P不在直线l2时，x，y满足的条件为：
，请画出图形，猜想∠APO，∠PAB，∠POC的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
（1）求证：△ADE≌△ABF；
（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；
（3）若BC=8，DE=6，求△AEF的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知E、F是□ABCD对角线AC上的两点，且BE⊥AC，DF⊥AC.
(1)请写出图中全等三角形（不再添加辅助线）．
(2)求证：△ABE≌△CDF；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），在
和
中，
为边
上一点，
平分
，
，
.
（1）求证：
（2）如图（2），若
，连接
交于
，
为边
上一点，满足
，连接
交于
. ①求
的度数；
②若
平分
，试说明：平分
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
