
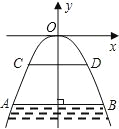
【题目】如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
【答案】(1)y=-![]() x2(2)从正常水位开始,持续10小时到达警戒线
x2(2)从正常水位开始,持续10小时到达警戒线
【解析】
(1)首先设所求抛物线的解析式为:y=ax2(a≠0),再根据题意得到C(-5,-1),利用待定系数法即可得到抛物线解析式;
(2)根据抛物线解析式计算出A点坐标,进而得到F点坐标,然后计算出EF的长,再算出持续时间即可.
解:(1)设所求抛物线的解析式为y=ax2.
∵CD=10 m,CD到拱桥顶E的距离仅为1 m,
∴C(-5,-1).
把点C的坐标代入y=ax2,
得a=-![]() ,
,
故抛物线的解析式为y=-![]() x2.
x2.
(2)∵AB宽20 m,
∴可设A(-10,b).
把点A的坐标代入抛物线的解析式y=-![]() x2中,
x2中,
解得b=-4,
∴点A的坐标为(-10,-4).
设AB与y轴交于点F,则F(0,-4),
∴EF=3 m.
∵水位以每小时0.3 m的速度上升,
∴3÷0.3=10(时).
答:从正常水位开始,持续10小时到达警戒线.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两种商品,已知买一件
两种商品,已知买一件![]() 商品要比买一件
商品要比买一件![]() 商品少30元,用160元全部购买
商品少30元,用160元全部购买![]() 商品的数量与用400元全部购买
商品的数量与用400元全部购买![]() 商品的数量相同.
商品的数量相同.
(1)求![]() 、
、![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() 、
、![]() 两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=-![]() ,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是直线x=﹣1.
(1)求m,n的值;
(2)x取什么值时,y随x的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5、-2、1、9,且任意相邻四个台阶上数的和都相等.
(1)求第5个台阶上的数![]() 是多少?
是多少?
(2)求从下到上前31个台阶上数的和;
(3)试用含![]() (
(![]() 为正整数)的式子表示出数“1”所在的台阶数.
为正整数)的式子表示出数“1”所在的台阶数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=Rt∠,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C恰好落在直线AB的边上的E处,若P是直线AD上的动点,则△PEB的周长最小值是____________ .
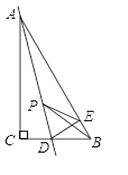
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平价商场经销甲、乙两种商品,甲种商品每件售价60元,得利润20元;乙种商品每件进价50元,售价80元.
(1)甲种商品每件进价为_____元,每件乙种商品所赚利润得百分数为_____%;
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件?
(3)在“元旦”期间,该商场只对甲、乙两种商品进行如下的优惠促销活动:
打折前一次性购物总金额 | 优惠措施 |
少于等于450 | 不优惠 |
超过450,但不超过600 | 按打九折 |
超过600 | 其中600部分八点二折优惠,超过600的部分打三折优惠 |
按上述优惠条件,若小华一次性购买乙种商品实际付款504元,求小华在该商场购买乙种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com