
【题目】现有![]() 、
、![]() 两种商品,已知买一件
两种商品,已知买一件![]() 商品要比买一件
商品要比买一件![]() 商品少30元,用160元全部购买
商品少30元,用160元全部购买![]() 商品的数量与用400元全部购买
商品的数量与用400元全部购买![]() 商品的数量相同.
商品的数量相同.
(1)求![]() 、
、![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() 、
、![]() 两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
【答案】(1)A商品每件20元,则B商品每件50元;(2)A商品6件,则购买B商品4件时所需总费用最低,最低费用为320元
【解析】
(1)设A商品每件x元,B商品每件y元,根据关系式列出二元一次方程组.
(2)设小亮准备A购买商品a件,则B购买商品![]() 件,根据关系式列出二元一次不等式方程组.求解再比较每方案的费用.
件,根据关系式列出二元一次不等式方程组.求解再比较每方案的费用.
解:(1)设![]() 商品每件
商品每件![]() 元,则
元,则![]() 商品每件
商品每件![]() 元,
元,
根据题意,得:![]() ,
,
经检验;![]() 是原方程的解,
是原方程的解,
所以A商品每件20元,则B商品每件50元.
(2)设购买![]() 商品
商品![]() 件,则购买
件,则购买![]() 商品共
商品共![]() 件,
件,
列不等式组:![]() ,
,
解得:![]() ,
,![]() 取整数:4,5,6.
取整数:4,5,6.
设购买总费用为![]() 元,则
元,则![]() ,
,
∵![]() ,∴
,∴![]() 随
随![]() 的增大而减小,∵
的增大而减小,∵![]() 的整数
的整数
∴当![]() 时,
时,![]() 取得最小值,最小值为320,
取得最小值,最小值为320,
答:当A商品6件,则购买B商品4件时所需总费用最低,最低费用为320元.


科目:初中数学 来源: 题型:
【题目】已知,如图,在等腰直角△ABC中,∠C=90°,AC=BC=4,点D是BC上一点,CD=1,点P是AB边上一动点,则PC+PD的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
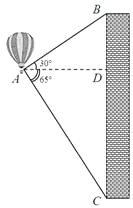
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在数学实践课中测量路灯的高度.如图,已知他的目高![]() 为1.5米,他先站在
为1.5米,他先站在![]() 处看路灯顶端
处看路灯顶端![]() 的仰角为
的仰角为![]() ,向前走3米后站在
,向前走3米后站在![]() 处,此时看灯顶端
处,此时看灯顶端![]() 的仰角为
的仰角为![]() (
(![]() ),则灯顶端
),则灯顶端![]() 到地面的距离约为( )
到地面的距离约为( )
A.3.2米B.4.1米C.4.7米D.5.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
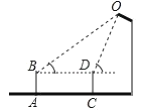
【题目】如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF.
求证:(1)△BDE≌△CDF;
(2)AD是△ABC的角平分线.
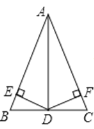
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E,AD=8,AB=16.
(1)求证:DE=BE;
(2)求S△BEF;
(3)若M、N分别为线段CD、DB上的动点,直接写出(NC+NM)的最小值___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
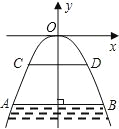
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com