
【题目】已知,如图,在等腰直角△ABC中,∠C=90°,AC=BC=4,点D是BC上一点,CD=1,点P是AB边上一动点,则PC+PD的最小值是________.

【答案】5
【解析】
过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP,此时DP+CP=DP+PC′=DC′的值最小.由DC=1,BC=4,得到BD=3,连接BC′,由对称性可知∠C′BE=∠CBE=45°,于是得到∠CBC′=90°,然后根据勾股定理即可得到结论.
过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP,
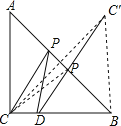
此时DP+CP=DP+PC′=DC′的值最小.
∵DC=1,BC=4,
∴BD=3,
连接BC′,由对称性可知∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=4,
根据勾股定理可得DC′=![]() =5.
=5.
故答案为:5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列调查方式正确的是( )
A.为了解七(1)班同学的课外兴趣爱好情况,采用抽样调查的方式.
B.为了解全区七年级学生对足球的爱好情况,采用抽样调查的方式.
C.为了解新生产的![]() 型药的药效情况,采用全面调查的方式.
型药的药效情况,采用全面调查的方式.
D.为了解深圳市民的业余生活情况,采用全面调查的方式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是 ( )
A. ∠A=∠C-∠B B. a2=b2-c2 C. a:b:c=2:3:4 D. a=![]() ,b=
,b=![]() ,c=1
,c=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程a2x2+(2a-1)x+1=0有两个不相等的实数根x1,x2.
(1)求a的取值范围;
(2)是否存在实数a,使方程的两个实数根互为相反数?如果存在,求出a的值;如果不存在,说明理由.
解:(1)根据题意,得Δ=(2a-1)2-4a2>0,解得a<![]() .∴当a<0时,方程有两个不相等的实数根. (2)存在.理由如下:如果方程的两个实数根x1,x2互为相反数,则x1+x2=-
.∴当a<0时,方程有两个不相等的实数根. (2)存在.理由如下:如果方程的两个实数根x1,x2互为相反数,则x1+x2=-![]() =0,① 解得a=
=0,① 解得a=![]() ,经检验,a=
,经检验,a=![]() 是方程①的根.∴当a=
是方程①的根.∴当a=![]() 时,方程的两个实数根x1与x2互为相反数.上述解答过程是否有错误?如果有,请指出错误之处,并解答.
时,方程的两个实数根x1与x2互为相反数.上述解答过程是否有错误?如果有,请指出错误之处,并解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】路桥方林汽车城某4S店销售某种型号的汽车,每辆车的进货价为15万元,市场调研表明:当销售价为21万元时,平均每周能售出6辆,而当销售价每降低0.5万元时,平均每周能多售出3辆,如果设每辆汽车降价x万元,平均每周的销售利润为W万元
(1)该4S店要想平均周获得72万元的销售利润,并且要尽可能地让利于顾客,则每辆汽车的定价应为多少万元?
(2)试写出W与x之间的函数关系式,并说明当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
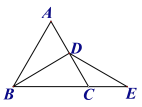
A.90°B.100°C.120°D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两种商品,已知买一件
两种商品,已知买一件![]() 商品要比买一件
商品要比买一件![]() 商品少30元,用160元全部购买
商品少30元,用160元全部购买![]() 商品的数量与用400元全部购买
商品的数量与用400元全部购买![]() 商品的数量相同.
商品的数量相同.
(1)求![]() 、
、![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() 、
、![]() 两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com