
����Ŀ��·�ŷ���������ij4S������ij���ͺŵ�������ÿ�����Ľ�����Ϊ15��Ԫ���г����б����������ۼ�Ϊ21��Ԫʱ��ƽ��ÿ�����۳�6�����������ۼ�ÿ����0.5��Ԫʱ��ƽ��ÿ���ܶ��۳�3���������ÿ����������x��Ԫ��ƽ��ÿ�ܵ���������ΪW��Ԫ
��1����4S��Ҫ��ƽ���ܻ��72��Ԫ������������Ҫ�����ܵ������ڹ˿ͣ���ÿ�������Ķ���ӦΪ������Ԫ��
��2����д��W��x֮��ĺ�����ϵʽ����˵����ÿ�������Ķ���Ϊ������Ԫʱ��ƽ��ÿ�ܵ��������������������Ƕ�����Ԫ��
���𰸡�(1) 18��Ԫ��(2) ÿ�������Ķ���Ϊ![]() ��Ԫʱ����ÿ�ܵ���������������������
��Ԫʱ����ÿ�ܵ���������������������![]() ��Ԫ.
��Ԫ.
��������
(1)������������=һ������������������������,һ������������=�ۼ�-����,�����ۼ۵�ͬʱ,�������ͻ����,��һ��һ�ӡ�,����ÿ����ӯ�����۵ļ�����Ԫ,�����з������;
(2)������������=һ������������������������,�����г�������ϵʽ,Ȼ��ȷ�����ֵ.
��1����ÿ�������Ľ���Ϊx��Ԫ����������ã�
��21��x��15����6+6x��=72��
���x1=2��x2=3��
�߾����ܵ������ڹ˿ͣ���x=3��
��ÿ�������Ķ���ӦΪ18��Ԫ��
��2����������ã�
W=��21��x��15����6+6x��=��x2+5x+6��
����W=����x��![]() ��2+
��2+![]() ��
��
�൱x=![]() ʱ��W���=
ʱ��W���=![]() ��
��
��ÿ�������Ķ���Ϊ![]() ��Ԫʱ����ÿ�ܵ���������������������
��Ԫʱ����ÿ�ܵ���������������������![]() ��Ԫ
��Ԫ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��600�����μ���Ʒ������Ϊÿ��6Ԫ����һ����ÿ��10Ԫ�ļ۸��۳�200�����ڶ�������ÿ��10Ԫ�ļ۸������Կ��۳�200�������̵�Ϊ���ʵ����������������������ۣ������г����飬����ÿ����1Ԫ���ɶ��۳�50�������ۼ۲��õ��ڽ��ۣ������۽���xԪ��������һ�ܺ��̵��ʣ�����μ���Ʒ��ִ�������ÿ��4Ԫ�ļ۸�ȫ���۳�������������μ���Ʒ������1250Ԫ���ʵڶ���ÿ�����μ���Ʒ�����ۼ۸�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺��һ�������ڽ���ȵ��ı��ν��������ڽ��ı��Ρ�.�����������⣺
(1)�����Ρ������Ρ������Ρ��С����ڽ��ı��Ρ���____________��
(2)��ͼ![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() .��֤���ı���
.��֤���ı���![]() �ǡ����ڽ��ı��Ρ���
�ǡ����ڽ��ı��Ρ���
(3)��֪���ڡ����ڽ��ı��Ρ�![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���뻭����Ӧͼ�Σ���ֱ��д��
���뻭����Ӧͼ�Σ���ֱ��д��![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڵ���ֱ����ABC�У���C=90����AC=BC=4,��D��BC��һ�㣬CD=1����P��AB����һ���㣬��PC+PD����Сֵ��________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����A����1��0������B��3��0������C��4��y1��������D��x2��y2����������������һ�㣬�����н��ۣ�
�ٶ��κ���y=ax2+bx+c����СֵΪ��4a��
������1��x2��4����0��y2��5a��
����y2��y1����x2��4��
��һԪ���η���cx2+bx+a=0��������Ϊ��1��![]()
������ȷ���۵ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ش��������⣺
��1��2317000�ÿ�ѧ��������ʾ��_______��
��2��2.5678��ȷ���ٷ�λ�Ľ�������________��
��3��������![]() ��ȷ��_______λ��
��ȷ��_______λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC��D��BC���е㣬��ACΪ������������ֱ����ACE����EAC=90��������BE����AD�ڵ�F����AC�ڵ�G��
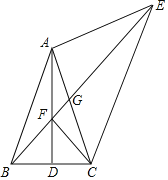
��1������BAC=50�������AEB�Ķ�����
��2����֤����AEB=��ACF��
��3�����ж��߶�EF��BF��AC����֮��ĵ�����ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����6�֣���ͼ���������̽������ʾ����������A����һ����¥����B������Ϊ30�������ⶰ��¥�ײ�C�ĸ���Ϊ65�������������¥��ˮƽ����ADΪ120m�����ⶰ��¥�ĸ߶ȣ�������ú�������ǵ����Ǻ�������ʽ��ʾ���ɣ�
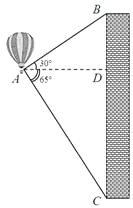
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ų�����ֽƬABCD�ضԽ���BD���ۣ�ʹ�õ�C���ڵ�F����DF��AB��E��AD=8��AB=16.
��1����֤��DE=BE��
��2����S��BEF��
��3����M��N�ֱ�Ϊ�߶�CD��DB�ϵĶ��㣬ֱ��д����NC+NM������Сֵ___________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com