练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

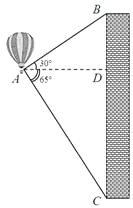
    【题目】（6分）如图，热气球的探测器显示，从热气球A处看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为65°，热气球与高楼的水平距离AD为120m．求这栋高楼的高度．（结果用含非特殊角的三角函数及根式表示即可）

    【答案】（40+120·tan65°）米

    【解析】

    试题根据Rt△ABD中∠BAD的正切值得出BD的长度，根据Rt△ACD中∠CAD的正切值得出CD的长度，然后根据BC=BD+CD得出答案．

    试题解析：在Rt△ABD中， ∵tan30°=∴BD=AD·tan30°=120×= 40

    在Rt△ACD中, ∵tan65°=∴CD=120·tan65°

    ∴BC=BD+CD=40+120·tan65°

    答：这栋高楼的高度为（40+120·tan65°）米

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】按要求解方程.

    (1)y(y-2)=3y2-1(公式法)； (2)(2x-1)2-3(2x-1)+2=0(因式分解法).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】路桥方林汽车城某4S店销售某种型号的汽车，每辆车的进货价为15万元，市场调研表明：当销售价为21万元时，平均每周能售出6辆，而当销售价每降低0.5万元时，平均每周能多售出3辆，如果设每辆汽车降价x万元，平均每周的销售利润为W万元

    （1）该4S店要想平均周获得72万元的销售利润，并且要尽可能地让利于顾客，则每辆汽车的定价应为多少万元？

    （2）试写出W与x之间的函数关系式，并说明当每辆汽车的定价为多少万元时，平均每周的销售利润最大？最大利润是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】等边三角形ABC 中，BD是角平分线，点E在BC边的延长线上，且CD=CE，则∠BDE的度数是（ ）

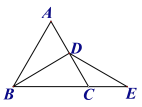
    A.90°B.100°C.120°D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请解答下列各题：

    （1）数轴上表示和的两点和之间的距离表示为_______，如果，那么_______．

    （2）若点表示的整数为，则当________时，．

    （3）要使取最小值时，相应的的取值范围是________，最小值是________．

    （4）已知，则的最大值为_______，最小值为_______．

    （5）若，则的取值范围是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2017年6月22日至7月2日，11天湖南地区持续降大到暴雨，总量达570亿立方米的雨水从天而降，倾泻到三湘大地，全省14个市州120个县（市、区）1621个多镇受灾，现有三批救灾物资从长沙岀发送往某受灾乡镇，前两批物资运货情况如图所示：

    火车皮（单位：节）

    汽车（单位：辆）

    物质重量（单位：吨）

    第一批

    4

    16

    264

    第二批

    6

    10

    340

    （1）每节火车皮和每辆汽车平均各能装多少吨物资？

    （2）已知火车皮的装运费为30元吨，汽车的装运费为100元/吨．若第三批救灾物资需要5节火车皮和15辆汽车正好装完，共需要装运费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

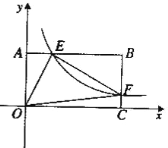
    【题目】如图22，将—矩形OABC放在直角坐际系中，O为坐标原点．点A在x轴正半轴上．点E是边AB上的—个动点(不与点A、N重合)，过点E的反比例函数的图象与边BC交于点F。

    【1】若△OAE、△OCF的而积分别为S1、S2．且S1＋S2=2，求的值：

    【2】若OA=2．0C=4．问当点E运动到什么位置时，四边形OAEF的面积最大．其最大值为多少?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有、两种商品，已知买一件商品要比买一件商品少30元，用160元全部购买商品的数量与用400元全部购买商品的数量相同．

    （1）求、两种商品每件各是多少元？

    （2）如果小亮准备购买、两种商品共10件，总费用不超过380元，且不低于300元，则如何购买才能使总费用最低？最低费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2＋bx＋c的图象如图，对称轴是直线x＝－，有下列结论：(1)ab＞0；(2)a＋b＋c＜0；(3)b＋2c＜0；(4)a－2b＋4c＞0.其中正确结论的个数是(　　)

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    同步练习册答案