
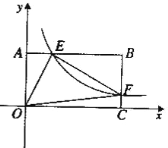
【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数![]() 的图象与边BC交于点F。
的图象与边BC交于点F。
【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求![]() 的值:
的值:
【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
【答案】
【1】∵点E、F在函数![]() 的图象上,
的图象上,
∴设E(![]() ,
, ![]() ),F(
),F(![]() ,
,![]() ),
),![]() >0,
>0,![]() >0,
>0,
∴S1=![]() ,S2=
,S2=![]() 。∵S1+S2=2,∴
。∵S1+S2=2,∴ ![]() 。∴
。∴![]() 。…………4分
。…………4分
【2】∵四边形OABC为矩形,OA=2,OC=4,∴设 E(![]() ,2), F(4,
,2), F(4,![]() )。∴BE=4-
)。∴BE=4-![]() ,BF=2-
,BF=2-![]() 。
。
∴S△BEF= ![]() ,S△OCF=
,S△OCF= ![]() ,S矩形OABC=2×4=8,
,S矩形OABC=2×4=8,
∴S四边形OAEF=S矩形OABC-S△BEF-S△OCF= 8-(![]() )-
)-![]() =
=![]() 。
。
∴当![]() =4时,S四边形OAEF=5。∴AE=2。
=4时,S四边形OAEF=5。∴AE=2。
∴当点E运动到AB的中点时,四边形OAEF的面积最大,最大值是5。…………………10分
【解析】(1)设E(x1,![]() ),F(x2,
),F(x2,![]() ),x1>0,x2>0,根据三角形的面积公式得到S1=S2=
),x1>0,x2>0,根据三角形的面积公式得到S1=S2= ![]() k,利用S1+S2=2即可求出k;
k,利用S1+S2=2即可求出k;
(2)设E(![]() ,2),F(4,
,2),F(4,![]() ),利用S四边形OAEF=S矩形OABC-S△BEF-S△OCF=-
),利用S四边形OAEF=S矩形OABC-S△BEF-S△OCF=-![]() (k-4)2+5,根据二次函数的最值问题即可得到当k=4时,四边形OAEF的面积有最大值,S四边形OAEF=5,此时AE=2.
(k-4)2+5,根据二次函数的最值问题即可得到当k=4时,四边形OAEF的面积有最大值,S四边形OAEF=5,此时AE=2.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:有一组相邻内角相等的凸四边形叫做“等邻角四边形”.请解答下列问题:
(1)“梯形、长方形、正方形”中“等邻角四边形”是____________;
(2)如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是“等邻角四边形”;
是“等邻角四边形”;
(3)已知:在“等邻角四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,请画出相应图形,并直接写出
,请画出相应图形,并直接写出![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
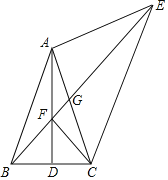
(1)若∠BAC=50°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)试判断线段EF、BF与AC三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
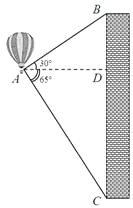
【题目】(6分)如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度.(结果用含非特殊角的三角函数及根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣4x+4与x轴、y轴分别交于A.B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线y=kx-1上,将该正方形沿x轴负方向平移a个单位长度后,顶点C恰好落在双曲线y=kx-1上,则a的值是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在数学实践课中测量路灯的高度.如图,已知他的目高![]() 为1.5米,他先站在
为1.5米,他先站在![]() 处看路灯顶端
处看路灯顶端![]() 的仰角为
的仰角为![]() ,向前走3米后站在
,向前走3米后站在![]() 处,此时看灯顶端
处,此时看灯顶端![]() 的仰角为
的仰角为![]() (
(![]() ),则灯顶端
),则灯顶端![]() 到地面的距离约为( )
到地面的距离约为( )
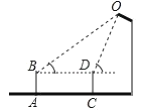
A.3.2米B.4.1米C.4.7米D.5.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E,AD=8,AB=16.
(1)求证:DE=BE;
(2)求S△BEF;
(3)若M、N分别为线段CD、DB上的动点,直接写出(NC+NM)的最小值___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是直线x=﹣1.
(1)求m,n的值;
(2)x取什么值时,y随x的增大而减小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com