
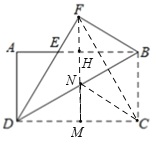
【题目】如图,把一张长方形纸片ABCD沿对角线BD对折,使得点C落在点F处,DF交AB于E,AD=8,AB=16.
(1)求证:DE=BE;
(2)求S△BEF;
(3)若M、N分别为线段CD、DB上的动点,直接写出(NC+NM)的最小值___________.

【答案】(1)证明见解析;(2)S△BDE=40;(3)12.8.
【解析】
(1)由折叠的性质可得到∠BDC=∠BDF,再由平行线的性质可得∠ABD=∠BDC,由此可得∠ABD=∠BDF,据此即可得结论;
(2)设BE=x,则DE=BE=x,AE=16-x,利用勾股定理即可求出BE的长,再利用三角形面积公式进行求解即可得答案;
(3)由题意知C、F关于直线BD对称,过点F作FM⊥CD,垂足为M,交BD于点N,交AB于点H,此时MN+NC的值最小,求出FH的长即可求得答案.
(1)∵△BCD≌△BFD,
∴∠BDC=∠BDF,
又∵四边形ABCD是长方形,
∴AB∥DC,
∴∠ABD=∠BDC,
∴∠ABD=∠BDF,
∴DE=BE;
(2)∵四边形ABCD是矩形,
∴∠A=90°,
∴AD2+AE2=DE2,
设BE=x,则DE=BE=x,AE=AB-BE=16-x,
∴82+(16-x)2=x2,
∴x=10,
∴S△BDE=![]() =40;
=40;
(3)由题意知C、F关于直线BD对称,过点F作FM⊥CD,垂足为M,交BD于点N,交AB于点H,此时MN+NC的值最小,
∵四边形ABCD是矩形,
∴AB//CD,∠A=∠ADM=90°,
∵FM⊥CD,
∴∠FMD=90°,
∴四边形ADMH是矩形,
∴∠FHE=90°,HM=AD=8,
∵∠A=∠BFE=90°,AD=BF,DE=BE,
∴Rt△ADE≌Rt△FBE(HL),
∴EF=AE=16-10=6,
∵S△BEF=![]() ,
,
∴FH=![]() =4.8,
=4.8,
∴FM=FH+HM=4.8+8=12.8,
即NC+NM的最小值为12.8,
故答案为:12.8.


科目:初中数学 来源: 题型:
【题目】路桥方林汽车城某4S店销售某种型号的汽车,每辆车的进货价为15万元,市场调研表明:当销售价为21万元时,平均每周能售出6辆,而当销售价每降低0.5万元时,平均每周能多售出3辆,如果设每辆汽车降价x万元,平均每周的销售利润为W万元
(1)该4S店要想平均周获得72万元的销售利润,并且要尽可能地让利于顾客,则每辆汽车的定价应为多少万元?
(2)试写出W与x之间的函数关系式,并说明当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
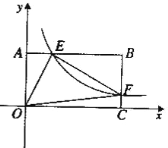
【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数![]() 的图象与边BC交于点F。
的图象与边BC交于点F。
【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求![]() 的值:
的值:
【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两种商品,已知买一件
两种商品,已知买一件![]() 商品要比买一件
商品要比买一件![]() 商品少30元,用160元全部购买
商品少30元,用160元全部购买![]() 商品的数量与用400元全部购买
商品的数量与用400元全部购买![]() 商品的数量相同.
商品的数量相同.
(1)求![]() 、
、![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() 、
、![]() 两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为圆
为圆![]() 的直径,
的直径,![]() 为圆
为圆![]() 上一点,
上一点,![]() 为
为![]() 延长线一点,且
延长线一点,且![]() ,
,![]() 于点
于点![]() .
.
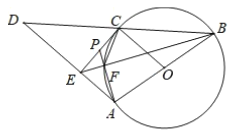
(1)求证:直线![]() 为圆
为圆![]() 的切线;
的切线;
(2)设![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,
,
①求证:![]()
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
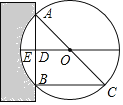
【题目】《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”
如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图,对称轴是直线x=-![]() ,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )
,有下列结论:(1)ab>0;(2)a+b+c<0;(3)b+2c<0;(4)a-2b+4c>0.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
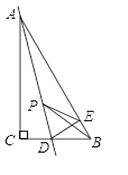
【题目】如图,在Rt△ABC中,∠C=Rt∠,∠ABC=60°,D是BC边上的点,CD=1,将△ACD沿直线AD翻折,点C恰好落在直线AB的边上的E处,若P是直线AD上的动点,则△PEB的周长最小值是____________ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com