
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
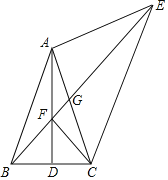
(1)若∠BAC=50°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)试判断线段EF、BF与AC三者之间的等量关系,并证明你的结论.
【答案】(1)20°;(2)证明见解析;(3)EF2+BF2=2AC2.理由见解析.
【解析】
(1)根据等腰直角三角形的旋转得出∠ABE=∠AEB,求出∠BAE,根据三角形内角和定理求出即可;
(2)根据等腰三角形的性质得出∠BAF=∠CAF,根据SAS推出△BAF≌△CAF,根据全等得出∠ABF=∠ACF,即可得出答案;
(3)根据全等得出BF=CF,求出∠CFG=∠EAG=90°,根据勾股定理求出EF2+BF2=EF2+CF2=EC2,EC2=AC2+AE2=2AC2,即可得出答案.
(1)∵AB=AC,△ACE是等腰直角三角形,
∴AB=AE,
∴∠ABE=∠AEB,
又∵∠BAC=50°,∠EAC=90°,
∴∠BAE=50°+90°=140°,
∴∠AEB=(180°-140°)÷2=20°;
(2)∵AB=AC,D是BC的中点,
∴∠BAF=∠CAF.
在△BAF和△CAF中
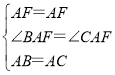 ,
,
∴△BAF≌△CAF(SAS),
∴∠ABF=∠ACF,
∵∠ABE=∠AEB,
∴∠AEB=∠ACF;
(3)∵△BAF≌△CAF,
∴BF=CF,
∵∠AEB=∠ACF,∠AGE=∠FGC,
∴∠CFG=∠EAG=90°,
∴EF2+BF2=EF2+CF2=EC2,
∵△ACE是等腰直角三角形,
∴∠CAE=90°,AC=AE,
∴EC2=AC2+AE2=2AC2,
即EF2+BF2=2AC2.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=120°,点 D 是 BC 上一点,BD 的垂直平分线交 AB 于点E,将△ACD 沿 AD 折叠,点 C 恰好与点 E 重合,则∠B 等于_______°;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】路桥方林汽车城某4S店销售某种型号的汽车,每辆车的进货价为15万元,市场调研表明:当销售价为21万元时,平均每周能售出6辆,而当销售价每降低0.5万元时,平均每周能多售出3辆,如果设每辆汽车降价x万元,平均每周的销售利润为W万元
(1)该4S店要想平均周获得72万元的销售利润,并且要尽可能地让利于顾客,则每辆汽车的定价应为多少万元?
(2)试写出W与x之间的函数关系式,并说明当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC 中,BD是角平分线,点E在BC边的延长线上,且CD=CE,则∠BDE的度数是( )
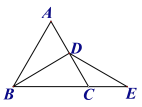
A.90°B.100°C.120°D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请解答下列各题:
(1)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离表示为_______,如果
之间的距离表示为_______,如果![]() ,那么
,那么![]() _______.
_______.
(2)若点![]() 表示的整数为
表示的整数为![]() ,则当
,则当![]() ________时,
________时,![]() .
.
(3)要使![]() 取最小值时,相应的
取最小值时,相应的![]() 的取值范围是________,最小值是________.
的取值范围是________,最小值是________.
(4)已知![]() ,则
,则![]() 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.
(5)若![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
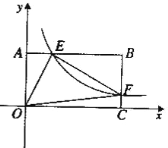
【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数![]() 的图象与边BC交于点F。
的图象与边BC交于点F。
【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求![]() 的值:
的值:
【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com