
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
【答案】D
【解析】∵抛物线![]() 顶点坐标为(0,
顶点坐标为(0, ![]() ),
),
半径为5的⊙O与y轴负半轴交点为(0,-5),
∴当y=0时,x=±1,∴整点为(1,0),(0,0),(-1,0);
当y=-1,x=±2,∴整点为(2,-1),(-1,-1),(0,-1),(1,-1),(2,-1);
当y=-2,x=±![]() ,∴整点为(2,-2),(-1,-2),(0,-2),(1,-2),(2,-2);
,∴整点为(2,-2),(-1,-2),(0,-2),(1,-2),(2,-2);
当y=-3,x=±![]() ,∴整点为(3,-3),(2,-3),(1,-3),(0,-3),(-1,-3),(-2,-3),(-3,-3);
,∴整点为(3,-3),(2,-3),(1,-3),(0,-3),(-1,-3),(-2,-3),(-3,-3);
当y=-4,x=±![]() ,∴整点为(3,-4),(2,-4),(1,-4),(0,-4),(-1,-4),(-2,-4),(-3,-4);
,∴整点为(3,-4),(2,-4),(1,-4),(0,-4),(-1,-4),(-2,-4),(-3,-4);
当y=-5,x=±4,∴整点为(4,-5),(3,-5),(2,-5),(1,-5),(0,-5),(-1,-5),(-2,-5),(-3,-5),(4,-5);
所以在阴影部分(不包括边界)的整点为:(0,0),(-1,-1),(0,-1),(1,-1),(-1,-2),(0,-2),(1,-2),(3,-3),(2,-3),(1,-3),(0,-3),(-1,-3),(-2,-3),(-3,-3),(3,-4),(2,-4),(1,-4),(0,-4),(-1,-4),(-2,-4),(-3,-4),故整点为21个.
故选:D.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价4元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2![]() )时,求∠ODB的正切值.
)时,求∠ODB的正切值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线试纸y=ax2+bx+c与x轴交于点A,C,与y轴交于点B.已知点A坐标为(8,0),点B为(0,8),点D为(0,3),tan∠DCO=![]() ,直线AB和直线CD相交于点E.
,直线AB和直线CD相交于点E.
⑴ 求抛物线的解析式,并化成y=a(x-m)2+h的形式;
⑵ 设抛物线的顶点为G,请在直线AB上方的抛物线上求点P的坐标,使得S△ABP=S△ABG.
⑶ 点M为直线AB上的一点,过点M作x轴的平行线分别交直线AB,CD于点M,N,连结DM,DN,是否存在点M,使得△DMN为等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
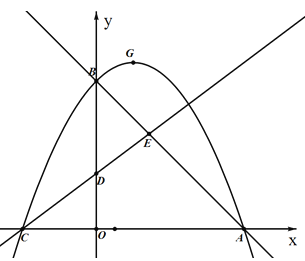
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)当t=3时四边形OQCD的面积为多少?
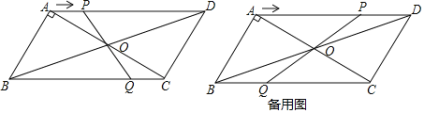
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:

(1)请估计:当![]() 很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率
很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率![]() .
.
(2)试估算盒子里白、黑两种颜色的球各有多少只?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com