
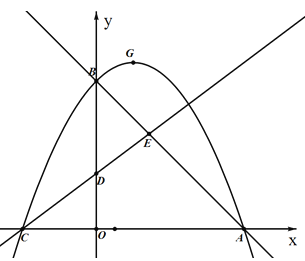
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���������ֽy=ax2+bx+c��x�ύ�ڵ�A,C����y�ύ�ڵ�B.��֪��A����Ϊ(8��0)����BΪ(0��8)����DΪ��0��3����tan��DCO=![]() ��ֱ��AB��ֱ��CD�ཻ�ڵ�E.
��ֱ��AB��ֱ��CD�ཻ�ڵ�E.
�� �������ߵĽ���ʽ��������y=a(x-m)2+h����ʽ��
�� �������ߵĶ���ΪG������ֱ��AB�Ϸ��������������P�����꣬ʹ��S��ABP=S��ABG.
�� ��MΪֱ��AB�ϵ�һ�㣬����M��x���ƽ���߷ֱ�ֱ��AB��CD�ڵ�M��N������DM��DN���Ƿ���ڵ�M��ʹ����DMNΪ���������Σ������ڣ��������M�����ꣻ�������ڣ���˵������.
���𰸡���1��![]() ����2��M��20��-12����M��
����2��M��20��-12����M��![]() ��
�� ![]() ���� M��-
���� M��-![]() ��
�� ![]() ��
��
�������������������1����Rt��DOC�У������пɵõ�C���꣬�������ߵĽ���ʽΪ![]() ���ѵ�B������룬��a��ֵ�����ɵ������߽���ʽ���ٻ�Ϊ����ʽ���ɣ�
���ѵ�B������룬��a��ֵ�����ɵ������߽���ʽ���ٻ�Ϊ����ʽ���ɣ�
��2�����P���꣬����P��PF��y�ύֱ��AB��F����AB������ɵó�ֱ��AB�Ľ���ʽ��
�ɴ˵�PF ,����G��GH��y�ύֱ��AB��H����GH=3����PF= GH=3�����xֵ��������õ�P���ꣻ
��3��������������ٵ�DM=DNʱ����DN=MNʱ�����M��ֵ����.
�����������1����Rt��DOC���� ![]() ����
����![]() ��
��
��OC=4 ��
��C(-4��0)��
��![]() ���ѵ�B��0,8�����룬��
���ѵ�B��0,8�����룬��![]() ��
��
��![]() ��
��![]() ��
��
![]() ��
��
��2����P��x�� ![]() ��������P��PF��y�ύֱ��AB��F��
��������P��PF��y�ύֱ��AB��F��
�� A��8,0����B��0,8��
��![]()
��F��x,-x+8��
��PF=![]() ��
��
����G��GH��y�ύֱ��AB��H����G��2,9����H��2,6��
��GH=3��
��PF= GH=3��
��![]() =3��
=3��
���![]() ����ȥ��
����ȥ��
��P��6,5����
��3����1�������
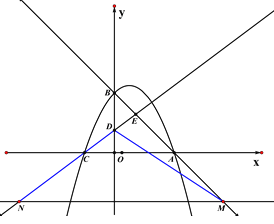
��DM=DNʱ��M��20��-12����
��M��m��-m+8������N��-m�� ![]() ����
����
��MN��x�ᣬ
�� -m+8=![]() ��
��
��m=20��
��2�������

��DN=MNʱ��M![]() M
M![]() ��
��
��M��m��-m+8������N��![]() ��-m+8����
��-m+8����
��![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵�����ܵõ�ֱ�������εģ� ��
A.�����Ƕ�֮��Ϊ 1��2��3 ��������B.�����߳�֮��Ϊ 3��4��5 ��������
C.�����߳�֮��Ϊ 8��16��17 ��������D.�����Ƕ�֮��Ϊ 1��1��2 ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c+2��ͼ����ͼ��ʾ������Ϊ����1��0�������н��ۣ���abc��0����b2��4ac=0����a��2����4a��2b+c��0��������ȷ���۵ĸ����ǣ� ��
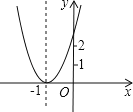
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����ǰѺᡢ�����궼�������ĵ��������.��ͼ����֪��O�İ뾶Ϊ5����������![]() ���Բ��Χ�ɵ���Ӱ���֣��������߽磩����������ǣ� ��
���Բ��Χ�ɵ���Ӱ���֣��������߽磩����������ǣ� ��

A. 24 B. 23 C. 22 D. 21
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
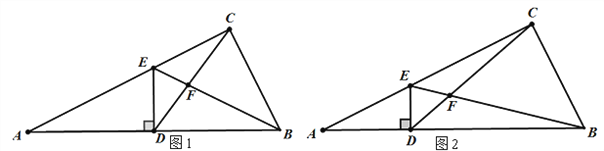
����Ŀ����ͼ1����DΪֱ��������ABC��б��AB�ϵ��е㣬DE��AB��AC��E, ��EB��CD���߶�CD��BF���ڵ�F.��tanA=![]() ,��
,��![]() =_____.��ͼ2����DΪֱ��������ABC��б��AB�ϵ�һ�㣬DE��AB��AC��E, ��EB��CD���߶�CD��BF���ڵ�F.��
=_____.��ͼ2����DΪֱ��������ABC��б��AB�ϵ�һ�㣬DE��AB��AC��E, ��EB��CD���߶�CD��BF���ڵ�F.��![]() ��tanA=
��tanA=![]() ����
����![]() =____.
=____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
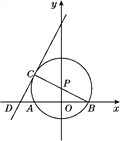
����Ŀ����ͼ����P��y��������P��x����A��B����������BP���ӳ�����P�ڵ�C������C��ֱ��y��2x��b��x���ڵ�D���ҡ�P�İ뾶Ϊ![]() ��AB��4.
��AB��4.
(1)���B��P��C�����ꣻ
(2)��֤��CD�ǡ�P��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ��������
��������![]() �ᡢ
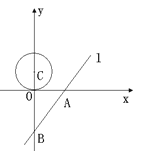
�ᡢ![]() ��ֱ���A��B���㣮һ���뾶Ϊ1.5�ġ�C��Բ��C�ӵ㣨0��1.5����ʼ��ÿ��0.5����λ���ٶ�����
��ֱ���A��B���㣮һ���뾶Ϊ1.5�ġ�C��Բ��C�ӵ㣨0��1.5����ʼ��ÿ��0.5����λ���ٶ�����![]() �������˶�������C��ֱ��
�������˶�������C��ֱ��![]() ����ʱ�����Բ�˶���ʱ��Ϊ��������
����ʱ�����Բ�˶���ʱ��Ϊ��������
A. 3���6�� B. 6�� C. 3�� D. 6���16��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
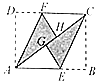
����Ŀ����ͼ���ھ���ֽƬ![]() �У�
��![]() ����
����![]() �ֱ���
�ֱ���![]() �ϣ���
�ϣ���![]() ��
��![]() ���ۣ�
���ۣ�![]() ������ǶԽ���
������ǶԽ���![]() �ϵĵ�
�ϵĵ�![]() ��
��![]() �����ı���
�����ı���![]() �������____________��
�������____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Լ������ƽ��ֱ������ϵ![]() �У�����������ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ�ߣ��иõ�ġ������ߡ������磬��
�У�����������ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ�ߣ��иõ�ġ������ߡ������磬��![]() �IJ������У�
�IJ�������![]() ��
��![]() ��
��![]() ��
��![]() ����ͼ1����
����ͼ1����
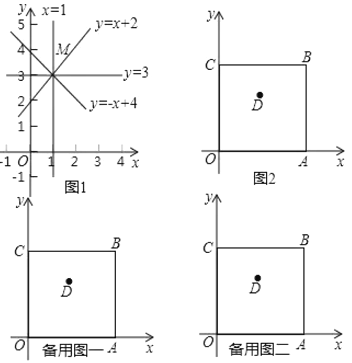
��ͼ2��������![]() ��ƽ��ֱ������ϵ
��ƽ��ֱ������ϵ![]() �У���
�У���![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() ��
��![]() �ֱ���
�ֱ���![]() ���
���![]() ���ϣ���
���ϣ���![]() ���������ڲ���
���������ڲ���
��1��ֱ��д����![]() �����в����ߣ� ��
�����в����ߣ� ��
��2����![]() ����
����![]() ���߶�
���߶�![]() �Ĵ�ֱƽ�����ϣ��ҵ�
�Ĵ�ֱƽ�����ϣ��ҵ�![]() ��һ����������
��һ����������![]() �����
�����![]() ��������_______________��
��������_______________��
��3���ڣ�2���������£���![]() ��
��![]() ��������һ�㣨��
��������һ�㣨��![]() �����
�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ����
����![]() ����
����![]() �۵�����
�۵�����![]() �Ķ�Ӧ���Ϊ
�Ķ�Ӧ���Ϊ![]() ������
������![]() �ڵ�
�ڵ�![]() ��ƽ����������IJ�������ʱ��д����Ӧ���ۺ�
��ƽ����������IJ�������ʱ��д����Ӧ���ۺ�![]() ����ֱ�ߵĽ���ʽ�� ��
����ֱ�ߵĽ���ʽ�� ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com