练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法不能得到直角三角形的（ ）

    A.三个角度之比为 1：2：3 的三角形B.三个边长之比为 3：4：5 的三角形

    C.三个边长之比为 8：16：17 的三角形D.三个角度之比为 1：1：2 的三角形

    【答案】C

    【解析】

    三角形内角和180°，根据比例判断A、D选项中是否有90°的角，根据勾股定理的逆定理判断B、C选项中边长是否符合直角三角形的关系.

    A中，三个角之比为1:2:3，则这三个角分别为：30°、60°、90°，是直角三角形；

    D中，三个角之比为1:1:2，则这三个角分别为：45°、45°、90°，是直角三角形；

    B中，三边之比为3:4:5，设这三条边长为：3x、4x、5x，满足：，是直角三角形；

    C中，三边之比为8:16:17，设这三条边长为：8x、16x、17x，，不满足勾股定理逆定理，不是直角三角形

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】小强骑车从家到学校要经过一段先上坡后下坡的路，在这段路上小强骑车的距离s(千米)与骑车的时间t（分钟）之间的函数关系如图所示，请根据图中信息回答下列问题：

    (1)小强去学校时下坡路长 千米；

    (2)小强下坡的速度为 千米/分钟；

    (3)若小强回家时按原路返回，且上坡的速度不变，下坡的速度也不变，那么回家骑车走这段路的时间是 分钟.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．

    （1）求∠C的大小；

    （2）求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一商店销售某种商品，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，该店采取了降价措施．在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

    （1）若降价4元，则平均每天销售数量为　 　件；

    （2）当每件商品降价多少元时，该商店每天销售利润为1050元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．

    （1）求证：BD=CE；

    （2）求证：∠M=∠N．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

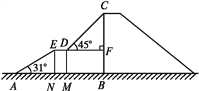
    【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲乙两人买了相同数量的信封和信笺，甲每发一封信都只用1张信笺，乙每发一封信都要用3张信笺，结果甲用掉了所有的信封，但余下50张信笺，而乙用掉了所有的信笺，但余下50个信封．

    (1)求甲乙两人各买的信封和信笺的数量分别为多少？

    (2)若甲乙两人每发出一封信需邮费5元，求甲乙各用去多少元邮费？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】大家见过形如x+y＝z，这样的三元一次方程，并且知道x＝3，y＝4，z＝7就是适合该方程的一个正整数解，法国数学家费尔马早在17世纪还研究过形如x2+y2＝z2的方程．

    （1）请写出方程x2+y2＝z2的两组正整数解：　 　．

    （2）研究直角三角形和勾股数时，我国古代数学专著（九章算术）给出了如下数：a＝（m2﹣n2），b＝mn，c＝（m2+n2），（其中m＞n，m，n是奇数），那么，以a，b，c为三边的三角形为直角三角形，请你加以验证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

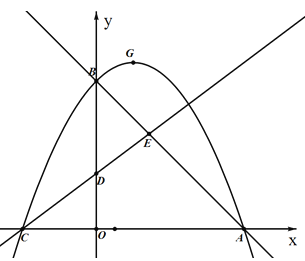
    【题目】如图，在平面直角坐标系中，抛物线试纸y=ax2+bx+c与x轴交于点A,C，与y轴交于点B.已知点A坐标为(8，0)，点B为(0，8)，点D为（0，3），tan∠DCO=，直线AB和直线CD相交于点E.

    ⑴ 求抛物线的解析式，并化成y=a(x-m)2+h的形式；

    ⑵ 设抛物线的顶点为G，请在直线AB上方的抛物线上求点P的坐标，使得S△ABP=S△ABG.

    ⑶ 点M为直线AB上的一点，过点M作x轴的平行线分别交直线AB，CD于点M，N，连结DM，DN，是否存在点M，使得△DMN为等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案