
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
科目:初中数学 来源: 题型:
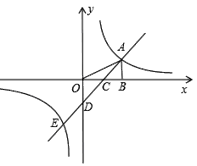
【题目】如图,在平面直角坐标系中,点A是反比例函数y=![]() (k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(1)分别求双曲线及直线AE的解析式;
(2)若点Q在双曲线上,且S△QAB=4S△BAC,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不能得到直角三角形的( )
A.三个角度之比为 1:2:3 的三角形B.三个边长之比为 3:4:5 的三角形
C.三个边长之比为 8:16:17 的三角形D.三个角度之比为 1:1:2 的三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
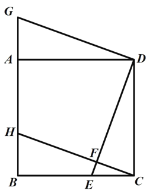
【题目】如图,四边形 ABCD 是正方形,点 E,H 分别在 BC,AB 上,点 G 在 BA 的延长线上, 且 CE=AG,DE⊥CH 于 F.
(1)求证:四边形 GHCD 为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF 互余的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() ,
,![]() 的方程组
的方程组![]() ,则下列结论中:①当
,则下列结论中:①当![]() 时,方程组的解是
时,方程组的解是![]() ;②当
;②当![]() ,
,![]() 的值互为相反数时,
的值互为相反数时,![]() ;③不存在一个实数
;③不存在一个实数![]() 使得
使得![]() ;④若
;④若![]() ,则
,则![]() 正确的个数有( )
正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
(1)求b,c,m的值;
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
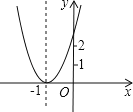
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com