
【题目】已知二次函数![]() 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
(1)求b,c,m的值;
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
【答案】(1)b=﹣1,c=﹣![]() ,m=﹣1;(2)P点坐标为(
,m=﹣1;(2)P点坐标为(![]() ,0).
,0).
【解析】试题分析:
(1)把点A、C的坐标代入![]() 列出关于b、c的二元一次方程组,解方程组即可得到b、c的值;再把所得b、c的值和点B的坐标代入
列出关于b、c的二元一次方程组,解方程组即可得到b、c的值;再把所得b、c的值和点B的坐标代入![]() 即可求得m的值;
即可求得m的值;
(2)由![]() 可得抛物线顶点的坐标为D(1,-2),对称轴为直线
可得抛物线顶点的坐标为D(1,-2),对称轴为直线![]() ;设抛物线对称轴和x轴交于点E,过点A(-3,6)作AF⊥x轴于点F,则易证△AFC和△DEC都是等腰直角三角形,从而可得∠PCD=∠ACB结合∠PDC=∠BAC,
;设抛物线对称轴和x轴交于点E,过点A(-3,6)作AF⊥x轴于点F,则易证△AFC和△DEC都是等腰直角三角形,从而可得∠PCD=∠ACB结合∠PDC=∠BAC,
△ABC∽△DPC,由此可解出PC的值,即可求得OP的值,从而可得点P的坐标.
试题解析:
(1)把A(﹣3,6)、C(3,0)代入解析式得: ![]() ,解得
,解得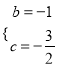 ,
,
∴抛物线的解析式为:y=![]() x2﹣x﹣
x2﹣x﹣![]() ,
,
当y=0,则![]() x2﹣x﹣
x2﹣x﹣![]() =0,解得,x1=3,x2=﹣1,
=0,解得,x1=3,x2=﹣1,
∵m<3,
∴m=﹣1,
∴ b=﹣1,c=﹣![]() ,m=﹣1;
,m=﹣1;
(2)由![]() 可得抛物线顶点的坐标为D(1,-2),对称轴为直线
可得抛物线顶点的坐标为D(1,-2),对称轴为直线![]() ,
,
设抛物线对称轴和x轴交于点E,过点A(-3,6)作AF⊥x轴于点F,
则DE=2,DC=OC-OD=2,AF=6,FC=3-(-3)=6,
∴DE=DC,AF=FC,
∴△AFC和△DEC都是等腰直角三角形,
∴∠PCD=∠ACB=45°,AC=![]() ,DC=
,DC=![]() ,
,
∵∠PDC=∠BAC,
∴△ABC∽△DPC,
∴![]() ,
,
∴BCDC=ACPC,即![]() ,
,
解得:PC=![]() ,则OP=
,则OP=![]() ,
,
所以P点坐标为![]() .
.


科目:初中数学 来源: 题型:
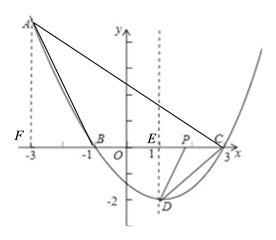
【题目】在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1.
查看答案和解析>>
科目:初中数学 来源: 题型:
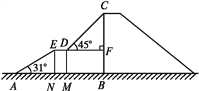
【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自 2019 年起逐月增加,据统计,该商城 9 月份销售自行车 64 辆,11 月份销售了 100 辆;
(1)若该商城 9 月至 11 月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共 100 辆,已知 A 型车的进价为每辆 500 元,售价为每辆 700 元,B 型车的进价为每辆 1000 元,售价为每辆 1300 元.假设所购进车辆全部售完,为使利润不低于 26000 元,该商城购进 A 型车不超过多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
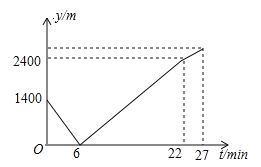
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com