
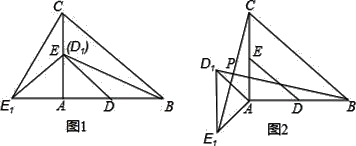
【题目】在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1.
【答案】(1)2![]() ; 2
; 2![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)利用等腰直角三角形的性质结合勾股定理分别得出BD1的长和CE1的长;
(2)根据旋转的性质得出,∠D1AB=∠E1AC=135°,进而求出△D1AB≌△E1AC(SAS),即可得出答案.
试题解析:(1)∵∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,
∴AE=AD=2,
∵等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),
∴当α=90°时,AE1=2,∠E1AE=90°,
∴BD1=![]() ,E1C=
,E1C=![]() ;
;
(2)证明:当α=135°时,如图2,
∵Rt△AD1E是由Rt△ADE绕点A逆时针旋转135°得到,
∴AD1=AE1,∠D1AB=∠E1AC=135°,
在△D1AB和△E1AC中
∵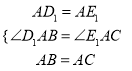 ,
,
∴△D1AB≌△E1AC(SAS),
∴BD1=CE1,且∠D1BA=∠E1CA,
记直线BD1与AC交于点F,
∴∠BFA=∠CFP,
∴∠CPF=∠FAB=90°,
∴BD1⊥CE1.


科目:初中数学 来源: 题型:
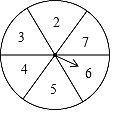
【题目】如图,现有一个转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)转到数字10是______(从“不确定事件”“必然事件”“不可能事件”选一个填入);
(2)转动转盘,转出的数字大于3的概率是______;
(3)现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).

(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 ;
(2)写出点A1 , B1 , C1的坐标(直接写答案), A1________ ,B1________ ,C1________;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
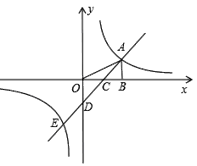
【题目】如图,在平面直角坐标系中,点A是反比例函数y=![]() (k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(1)分别求双曲线及直线AE的解析式;
(2)若点Q在双曲线上,且S△QAB=4S△BAC,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
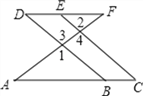
解:∵∠1=∠2(已知),∠1=∠3(______________),
∴∠2=∠3(___________________).
∴__∥__(__________________________________).
∴∠C=∠ABD (________________________________).
又∵∠C=∠D(____________),
∴∠D=∠ABD(等量代换)
∴AC∥DF(______________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
(1)求b,c,m的值;
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com