
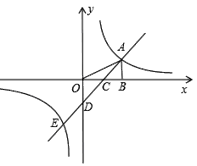
【题目】如图,在平面直角坐标系中,点A是反比例函数y=![]() (k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(k≠0)图象上一点,AB⊥x轴于B点,一次函数y=ax+b(a≠0)的图象交y轴于D(0,-2),交x轴于C点,并与反比例函数的图象交于A,E两点,连接OA,若△AOD的面积为4,且点C为OB中点.
(1)分别求双曲线及直线AE的解析式;
(2)若点Q在双曲线上,且S△QAB=4S△BAC,求点Q的坐标.
【答案】(1)y=x-2;(2)Q点的坐标为(12, ![]() )或(-4,-2).
)或(-4,-2).
【解析】试题分析:(1)先根据点D的坐标和△AOD的面积,求得点C的坐标,再结合点C为OB中点,求得点A的坐标,最后运用待定系数法求得反比例函数和一次函数的解析式;
(2)先设Q的坐标为(t, ![]() ),根据条件S△QAB=4S△BAC求得t的值,进而得到点Q的坐标.
),根据条件S△QAB=4S△BAC求得t的值,进而得到点Q的坐标.
试题解析:(1)∵D(0,-2),△AOD的面积为4,
∴![]() ×2×OB=4,
×2×OB=4,
∴OB=4,
∵C为OB的中点,
∴OC=BC=2,C(2,0)
又∵∠COD=90°
∴△OCD为等腰直角三角形,
∴∠OCD=∠ACB=45°,
又∵AB⊥x轴于B点,
∴△ACB为等腰直角三角形,
∴AB=BC=2,
∴A点坐标为(4,2),
把A(4,2)代入y=![]() ,得k=4×2=8,
,得k=4×2=8,
即反比例函数解析式为y=![]() ,
,
将C(2,0)和D(0,-2)代入一次函数y=ax+b,可得
![]() ,解得
,解得![]() ,
,
∴直线AE解析式为:y=x-2;
(2)设Q的坐标为(t, ![]() ),
),
∵S△BAC=![]() ×2×2=2,
×2×2=2,
∴S△QAB=4S△BAC=8,
即![]() ×2×|t-4|=8,
×2×|t-4|=8,
解得t=12或-4,
在y=![]() 中,当x=12时,y=
中,当x=12时,y=![]() ;当x=-4时,y=-2,
;当x=-4时,y=-2,
∴Q点的坐标为(12, ![]() )或(-4,-2).
)或(-4,-2).


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:

(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A为双曲线y=![]() (k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
(k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
A. 2![]() B. ±2
B. ±2![]() C.
C. ![]() D. ±
D. ±![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
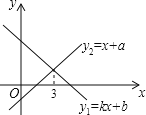
【题目】一次函数![]() 与
与![]() 的图象如图,则下列结论①
的图象如图,则下列结论①![]() ②
②![]() ,且
,且![]() 的值随着
的值随着![]() 值的增大而减小.③关于
值的增大而减小.③关于![]() 的方程
的方程![]() 的解是
的解是![]() ④当
④当![]() 时,
时,![]() ,其中正确的有___________.(只填写序号)
,其中正确的有___________.(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
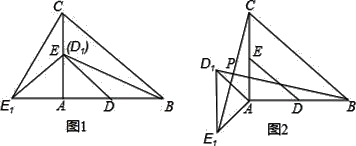
【题目】在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是边AB,AC的中点,若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1=CE1,且BD1⊥CE1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价4元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com