
【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

【答案】(1)见解析;(2)∠BOD =60°.
【解析】
(1)根据等腰直角三角形的性质,结合题意,由全等三角形的判断方法(SAS)得到三角形全等,再由全等三角形的性质得出答案;
(2)根据等边三角形的性质得出AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE,根据全等三角形的性质得出∠BEA=∠ACD,求出∠BOC=∠ECO+∠OEC=∠ACE+∠AEC,代入求出即可.
(1)证明:∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AE=AC,
又∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
在△ABE和△ADC中,
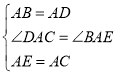 ,
,
∴△ABE≌△ADC(SAS),
∴BE=DC,∠ABE=∠ADC,
又∵∠BFO=∠DFA,∠ADF+∠DFA=90°,
∴∠ABE+∠BFO=90°,
∴∠BOF=∠DAF=90,
即BE⊥DC.
(2)解:结论:BE=CD.
理由:如图2,∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠ACE=∠AEC=60°,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
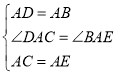 ,
,
∴△DAC≌△BAE(SAS),
∴CD=BE,∠BEA=∠ACD,
∴∠BOC=∠ECO+∠OEC
=∠DCA+∠ACE+∠OEC
=∠BEA+∠ACE+∠OEC
=∠ACE+∠AEC
=60°+60°
=120°.
∴∠BOD=180°-∠BOC=60°.


科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
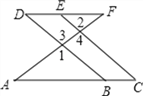
解:∵∠1=∠2(已知),∠1=∠3(______________),
∴∠2=∠3(___________________).
∴__∥__(__________________________________).
∴∠C=∠ABD (________________________________).
又∵∠C=∠D(____________),
∴∠D=∠ABD(等量代换)
∴AC∥DF(______________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
(1)求b,c,m的值;
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦前夕,湖州吴兴某工艺厂设计了一款成本10元/件的工艺品投放市场试销.试销发现,每天销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数:y=-10x+700. (利润=销售总价-成本总价)
⑴ 如果该厂想要每天获得5000元的利润,那么销售单价应定为多少元/件?
⑵ 当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
⑶ 湖州市物价部门规定,该工艺品销售单价最高不能超过38元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
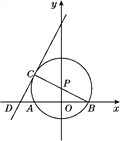
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
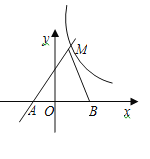
【题目】如图,直线y=kx+k(k≠0)与双曲线![]() 在第一象限内相交于点M,与x轴交于点A.
在第一象限内相交于点M,与x轴交于点A.
(1)求m的取值范围和点A的坐标;
(2)若点B的坐标为(3,0),AM=5,S△ABM=8,求双曲线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
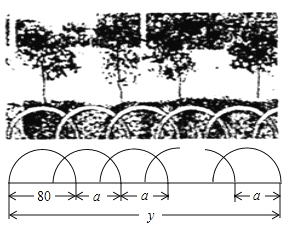
【题目】如图所示,某花园护栏是用直径为![]() 的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加
的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加![]() ,设半圆形条钢的个数为
,设半圆形条钢的个数为![]() (
(![]() 为正整数),护栏总长度为
为正整数),护栏总长度为![]() .
.
(1)若![]() .
.
①当![]() 时,y=______
时,y=______![]() ;
;
②写出![]() 与
与![]() 之间的函数关系式为_______.
之间的函数关系式为_______.
(2)若护栏总长度为![]() ,则当
,则当![]() 时,所用半圆形条钢个数为_______;
时,所用半圆形条钢个数为_______;
(3)若护栏总长度不变,则当![]() 时,用了
时,用了![]() 个半圆形条钢;当
个半圆形条钢;当![]() 时,用了
时,用了![]() 个半圆形条钢.请求出
个半圆形条钢.请求出![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com