
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=______.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,则∠AOC= .
如图(2)若∠BOD=35°,则∠AOC= .
(2)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(3)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直.(填空)
(3) 当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自 2019 年起逐月增加,据统计,该商城 9 月份销售自行车 64 辆,11 月份销售了 100 辆;
(1)若该商城 9 月至 11 月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共 100 辆,已知 A 型车的进价为每辆 500 元,售价为每辆 700 元,B 型车的进价为每辆 1000 元,售价为每辆 1300 元.假设所购进车辆全部售完,为使利润不低于 26000 元,该商城购进 A 型车不超过多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() ,求证:
,求证:![]() ,下面写出可运用反证法证明这个命题的四个步骤:
,下面写出可运用反证法证明这个命题的四个步骤:
①∴![]() ,这与三角形内角和为
,这与三角形内角和为![]() 矛盾,②因此假设不成立.∴
矛盾,②因此假设不成立.∴![]() ,③假设在
,③假设在![]() 中,
中,![]() ,④由
,④由![]() ,得
,得![]() ,即
,即![]() .这四个步骤正确的顺序应是( )
.这四个步骤正确的顺序应是( )
A.③④②①B.③④①②C.①②③④D.④③①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点O出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点![]() 的坐标为_______.
的坐标为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
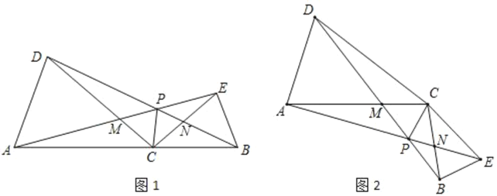
【题目】如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为 ;请直接写出∠APD= ;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com